나만의 작은 도서관
[알고리즘] parametric search와 lower bound, upper bound 본문
parametric search란?
parametric search는 최적화 문제를 결정 문제로 바꾼 뒤 이진 탐색을 이용해 최적해를 찾는 방식이다.
최적화 문제와 결정 문제
최적화 문제(mathematical optimization problem)는 주어진 조건을 만족하는 여러가지 해 중에서 가장 최적해를 구하는 문제이다. 우리가 접하는 대부분의 알고리즘 문제들이 최적화 문제이며, "OO을 만족하는 최솟값을 구하시오" 또는 "OO을 만족하는 최댓값을 구하시오" 와 같이 적혀있는게 특징이다.
결정 문제(decision problem)는 주어진 조건을 만족하는 해가 존재하는 지 여부를 구하는 문제로, YES 또는 NO 이렇게 단 두 가지의 결과만이 나온다는 것이 특징이다. 예로, "X라는 값이 배열 arr에 존재한다면 1, 그렇지 않다면 0을 출력하시오"와 같은 뉘앙스의 문제가 결정 문제이다.
lower bound, upper bound
parametric search를 이용한 대표적인 알고리즘이 바로 lower bound와 upper bound이다. lower bound와 upper bound는 직역하면 하한과 상한으로, 이름 그대로 정렬된 일련의 값들 중에서 임의의 값의 하한과 상한을 구하는 알고리즘이다. 여기서 하한은 임의의 값 k보다 크거나 같은 값 중 가장 낮은 위치(v[i - 1] < k <= v[i]을 만족하는 i), 상한은 임의의 값 k보다 큰 값의 위치 중 가장 낮은 위치(v[i - 1] <= k < v[i]을 만족하는 i)를 의미한다. 예를 들어, [10, 11, 11, 11, 12, 13] 과 같은 배열이 존재한다고 가정했을 때, 11의 lower bound는 1, upper bound는 4가 된다.
그림으로 표현하면 다음과 같다. 배열 아래 left/right는 '경계선 기준으로 어느 위치에 있는가?'를 표현한 것이다.
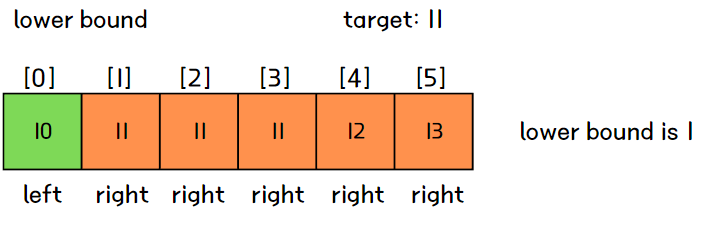
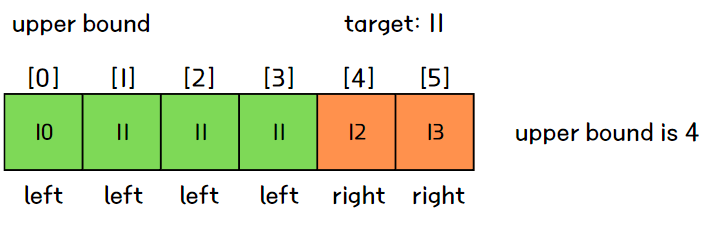
lower bound와 upper bound의 특징은 타겟값과 동일한 값이 많을수록 거리가 멀어진다는 특징이 있다. 예를 들어, 타겟값과 동일한 값이 배열에 1개 존재한다면 거리가 1만큼 차이나고, 3개 있다면 거리가 3만큼 차이난다. 즉, lower bound - upper bound = 타겟값과 동일한 값의 개수가 되며, 그렇기 때문에 lower bound의 위치와 upper bound의 위치가 같다면 타겟값과 동일한 값이 배열에 존재하지 않음을 의미한다.
lower bound, upper bound 동작방식
기본적인 동작방식은 이진 탐색과 동일하다. 다만, 특정한 값의 존재 유무를 알고 싶은 것이 아닌, 조건을 만족하는 위치를 알고 싶은 것이기 때문에 탐색 범위를 줄이는 코드를 변경해야한다.
1. 초기화

시작은 이진 탐색과 동일하게 start는 배열의 첫번째 위치, end는 배열의 마지막 위치 + 1로 초기화한다.
2. 범위 나누기

초기화 이후 탐색을 시작한다. 탐색 범위는 [start , end)가 되며, 탐색 범위의 중앙값을 기준으로 왼쪽, 오른쪽 범위로 나누어진다.
3. 대소비교 및 범위 변경


타겟값과 중앙값을 대소비교한다. 만약 타겟값이 중앙값보다 크다면, 중앙값보다 큰 수들이 존재하는 범위에서 찾아야하므로 탐색 범위를 오른쪽으로 변경한다. 반대로 타겟값이 중앙값보다 작으면, 중앙값보다 작은 수들이 존재하는 범위에서 찾아야하므로 탐색 범위를 왼쪽으로 변경한다.
여기서 처음으로 기존 이진 탐색과 다른 점이 발생하는데, 중앙값이 타겟값과 동일할 경우 lower bound는 왼쪽으로 줄이고, upper bound는 오른쪽으로 줄이게 된다.
탐색 범위를 변경했다면, 변경된 탐색 범위의 중앙값과 타겟값을 대소비교하는 작업을 반복한다.
4. 탐색 결과 반환

루프를 전부 돌고 start와 end의 값이 같아졌다면(탐색 가능한 범위가 0이됨) 해당 값의 index를 반환한다.
구현 코드
lower bound와 upper bound의 차이점은 타겟값과 동일한 값과 마주쳤을 때, 탐색 범위를 왼쪽으로 줄일 것이냐, 오른쪽으로 줄일 것이냐다. lower bound의 경우 왼쪽으로 줄이며, upper bound는 오른쪽으로 줄이기 때문에 각각의 조건문에 등호(=)가 들어가게 된다.
lower bound
int lowerBound(vector<int>& v, int target){
int start = 0, end = v.size();
while(start < end){
int mid = (start + end) / 2;
if(v[mid] < target){ // 오른쪽 범위로 줄여야 하는 경우(중앙값 < 타겟값)
start = mid + 1;
}
else{ // 왼쪽 범위로 줄여야 하는 경우(중앙값 >= 타겟값)
end = mid;
}
}
return start;
}
upper bound
int upperBound(vector<int>& v, int target){
int start = 0, end = v.size();
while(start < end){
int mid = (start + end) / 2;
if(v[mid] <= target){ // 오른쪽 범위로 줄여야 하는 경우(중앙값 <= 타겟값)
start = mid + 1;
}
else{ // 왼쪽 범위로 줄여야 하는 경우(중앙값 > 타겟값)
end = mid;
}
}
return start;
}
STL로 구현되어 있다.
C++ STL에 lower_bound, upper_bound라는 이름으로 함수가 구현되어 있다. <algorithm> 헤더에 포함되어 있으며, 리턴 값이 iterator임으로 index값을 구하려면 v.begin()처럼 처음 주소의 위치를 빼줘야하며, 값을 구하고 싶다면 *lb와 같이 '*'을 붙여줘야 한다.
int main()
{
vector<int> v1 = {10, 11, 11, 11, 12, 13};
int target = 11;
auto lb = lower_bound(v1.begin(), v1.end(), target);
auto ub = upper_bound(v1.begin(), v1.end(), target);
cout << "Lower bound idx is " << lb - v1.begin() << '\n';
cout << "Upper bound idx is " << ub - v1.begin() << '\n';
return 0;
}
// 실행 결과
Lower bound idx is 1
Upper bound idx is 4
STL 구현 코드
// lower bound
template<typename _ForwardIterator, typename _Tp, typename _Compare>
_ForwardIterator
__lower_bound(_ForwardIterator __first, _ForwardIterator __last,
const _Tp& __val, _Compare __comp)
{
typedef typename iterator_traits<_ForwardIterator>::difference_type
_DistanceType;
_DistanceType __len = std::distance(__first, __last);
while (__len > 0)
{
_DistanceType __half = __len >> 1;
_ForwardIterator __middle = __first;
std::advance(__middle, __half);
if (__comp(__middle, __val))
{
__first = __middle;
++__first;
__len = __len - __half - 1;
}
else
__len = __half;
}
return __first;
}
// upper bound
template<typename _ForwardIterator, typename _Tp, typename _Compare>
_ForwardIterator
__upper_bound(_ForwardIterator __first, _ForwardIterator __last,
const _Tp& __val, _Compare __comp)
{
typedef typename iterator_traits<_ForwardIterator>::difference_type
_DistanceType;
_DistanceType __len = std::distance(__first, __last);
while (__len > 0)
{
_DistanceType __half = __len >> 1;
_ForwardIterator __middle = __first;
std::advance(__middle, __half);
if (__comp(__val, __middle))
__len = __half;
else
{
__first = __middle;
++__first;
__len = __len - __half - 1;
}
}
return __first;
}
참고자료
https://blog.naver.com/jinhan814/222156334908
'C++ > 알고리즘' 카테고리의 다른 글
| [알고리즘] 너비 우선 탐색(BFS)와 dx, dy 테크닉 (0) | 2024.10.14 |
|---|---|
| [알고리즘] 백트래킹(backtracking)과 깊이 우선 탐색(DFS) (0) | 2024.10.13 |
| [알고리즘] 최대공약수(GCD)와 유클리드 호제법(Euclidean algorithm) (0) | 2024.10.12 |
| [알고리즘] 소수 판별법과 에라토스테네스의 체 (2) | 2024.10.11 |
| [알고리즘] 이진 탐색(Binary search) (0) | 2024.03.24 |





