나만의 작은 도서관
[알고리즘] 백트래킹(backtracking)과 깊이 우선 탐색(DFS) 본문
백트래킹이란?

백트래킹은 한국말로 "되추적"이라는 뜻으로, 이름에서 알 수 있듯 해답이 아닌 경우 이전 단계로 되돌아가 다른 경우를 선택하여 해답을 추적하는 방법이다. 백트래킹은 가능한 모든 경우를 탐색하기 때문에 완전 탐색(exhausted search) 알고리즘으로 분류되며, 일반적으로 상태공간트리(state space tree)나 그래프(graph)를 탐색할 때 사용한다.
상태공간트리란?
상태공간트리는 탐색 알고리즘에서 문제의 해결 과정을 트리 구조로 표현한 것이다. 노드는 특정 과정에서의 상태를, 마디(경로)는 문제를 해결하기 위해 선택된 일련의 결정들을 의미한다. 틱택토에 대한 상태공간트리를 그림으로 표현하면 다음과 같다.

상태공간트리의 탐색 시간복잡도: O(M^N)
백트래킹은 모든 경우의 수들을 탐색하는 완전 탐색 알고리즘이다. 위에서 예시로 든 틱택토에서 발생할 수 있는 모든 경우의 수들을 탐색하고 싶다면(중간에 승부가 나도 계속 진행한다) O 또는 X가 들어갈 자리가 9칸임으로 2^9개를 탐색해야 한다. 다른 예시로 같은 3*3 격자에서 O 또는 X가 아닌 1~9중 하나의 숫자가 들어가야 하는 경우라면 9가지의 숫자가 들어갈 자리가 9칸임으로 9^9 개를 탐색해야 한다. 즉, 검색 공간(search space)의 수가 N개이고, 각 검색 공간에서 선택 가능한 경우의 수가 M개일 때 전체 경우의 수는 M^N개로, 시간복잡도는 O(M^N)이 된다.
이렇듯 백트래킹은 지수의 시간복잡도를 가진 알고리즘이다보니 N과 M의 크기가 커질수록 연산 횟수가 기하급수적으로 늘어난다는 특징이 있다.
탐색의 효율성을 높이는 가지치기(pruning)
모든 경우의 수를 알아내는 것이 아닌 특정 조건을 만족하는 경우들을 찾는 것이라면 모든 경우의 수를 탐색할 필요는 없다. 일반적으로 해답이 될 가능성이 없는 마디를 유망하지 않다(nonpromising)고 하는데, 유망하지 않은 노드를 발견했을 때 탐색을 중단하고 해당 노드의 부모 노드로 되돌아감(백트래킹)으로써 탐색의 효율성을 높일 수 있다. 이러한 방식을 가지치기(pruning)라고 부른다. 아래 예시를 통해 알아보자.
여기 각 노드의 상태를 숫자로 표현한 상태공간트리가 있고, 백트래킹을 이용해 각 단계의 상태 노드가 0 또는 1로 이루어진 경우의 수들을 얻고 싶은 상황이라 가정해 보자.

만약 가지치기를 하지 않고 백트래킹을 했다면 모든 노드를 탐색하기 때문에 총 1+2+4+8 = 15개의 노드를 탐색해야 한다. 하지만, 가지치기를 통해 해답이 될 수 없는 유망하지 않은 노드에선 탐색을 중단함으로써 11개의 노드만 탐색해도 동일한 탐색 결과를 얻을 수 있다.

깊이 우선 탐색(DFS)
깊이 우선 탐색(DFS, Depth First Search)은 그래프를 탐색할 때 깊이와 너비 중 깊이를 우선적으로 탐색하는 방식을 말한다. 여기서 "깊이"는 루트 노드로부터 떨어진 거리를 말하며, "너비"는 같은 깊이에 있는 노드들의 수를 의미한다(간단하게 깊이는 수직, 너비는 수평이라고 보면 된다). 깊이 우선 탐색은 프리오더(preorder, root -> 왼쪽 -> 오른쪽 순으로 순회하는 방식)로 순회하는 것이 일반적이며, 앞서 알아본 백트래킹의 코드와 상당히 유사하다.
DFS를 이용한 그래프 탐색의 시간복잡도: O(V+E) or O(V^2)
깊이 우선 탐색은 모든 정점들을 탐색하는 것이 주목적이기 때문에 이를 중점으로 시간복잡도가 계산되어야 한다. 따라서 깊이 우선 탐색은 그래프가 어떻게 표현되었는가에 따라 시간복잡도가 다음과 같아진다.
그래프의 정점(Vertex) 수를 V, 간선(Edge) 수를 E라고 했을 때,
- 그래프가 인접 리스트로 표현된 경우 O(V + E)
- 그래프가 인접 행렬로 표현된 경우 O(V^2)
깊이 우선 탐색 동작방식
(보통 그래프에서는 정점, 트리에서는 노드라고 부른다. 하지만 계속 노드라고 적어왔으니 노드라고 부르겠다.)
1. 시작점 선택
탐색을 시작할 노드(다른 말로 정점)를 선택한다. 선택한 노드는 루트 노드(level 0)가 되며, 루트 노드를 방문하면서 탐색을 시작한다. 아래 예시에서는 시작점으로 0번 노드를 선택했다.
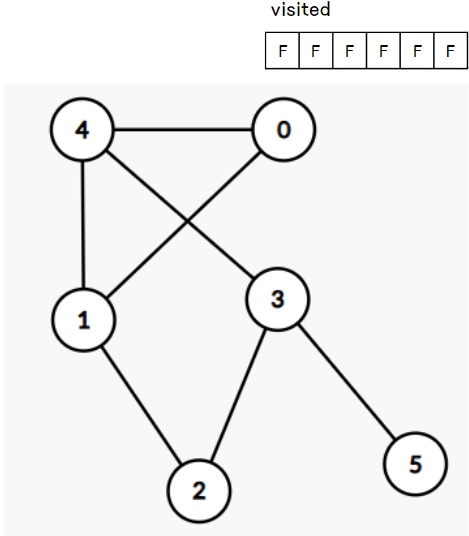
2. 방문 기록
노드를 방문했다면 방문한 사실을 기록한다. 방문 여부는 별도의 리스트(배열, 집합 등)를 통해 기록한다.

3. 인접 노드 탐색
현재 노드의 방문하지 않은 인접 노드들 중 가장 왼쪽에 있는 노드를 탐색한다. 만약 인접 노드들 중 방문 가능한 노드가 존재하지 않는다면 이전 노드로 되돌아간다.

4. 재귀 호출
2~3번 과정을 재귀 호출을 통해 모든 노드를 방문하거나 탐색 가능한 경로가 없을 때까지 반복한다.



5. 종료
모든 노드를 방문하거나 탐색할 경로가 없다면 탐색을 종료한다.

구현 코드(백트래킹)
문제: 백준 15654번 - N과 M(5)
https://www.acmicpc.net/problem/15654
int N, M;
vector<int> v1; // v1: 검색 공간을 담고있는 상태공간트리
vector<int> curState; // curState: 현재 상태
void backtracking(int size, int M){
// 해당 노드가 유망한지 판단(isPromising())
if(size > 0 && curState[size-1] == 0) return;
// 종료 조건
if(size == M){
for(int elem : curState){
cout << elem << ' ';
}
cout << '\n';
return;
}
for(int i = 0; i < N; i++){
curState[size] = v1[i];
v1[i] = 0; // 해당 숫자를 선택했다는 의미로 0 대입
backtracking(size+1, M); // 다음 상태 노드로 이동
v1[i] = curState[size]; // 해당 숫자를 선택하기 전으로 백트래킹
}
}
위 방법이 백트래킹을 이용하는 정석적인 방법이지만, 부모 노드에서 유망하지 않은 자식 노드로 매번 진입한다는 점이 비효율적이다. 따라서, 개인적으로 자식 노드 중 유망한 노드만 진입하는 아래와 같은 방식을 선호한다.
int N, M;
vector<int> v1; // v1: 검색 공간을 담고있는 상태공간트리
vector<int> curState; // curState: 현재 상태
void backtracking(int size, int M){
// 종료 조건
if(size == M){
for(int elem : curState){
cout << elem << ' ';
}
cout << '\n';
return;
}
for(int i = 0; i < N; i++){
if(v1[i] != 0){ // 해당 노드가 유망한지 판단(isPromising())
curState[size] = v1[i];
v1[i] = 0; // 해당 숫자를 선택했다는 의미로 0 대입
backtracking(size+1, M); // 다음 상태 노드로 이동
v1[i] = curState[size]; // 해당 숫자를 선택하기 전으로 백트래킹
}
}
}
구현 코드(DFS)
문제: 백준 1260번 - DFS와 BFS
https://www.acmicpc.net/problem/1260
vector<vector<int>> graph; // 인접 노드 방식
vector<bool> visited;
vector<int> path;
void dfs(int here){
// 방문 처리.
visited[here] = true;
path.push_back(here);
// 조건 만족시 실행
// if(isCondition){
// }
for(int there : graph[here]){
if(!visited[there]){
dfs(there);
}
}
return;
}
void dfsAll(){
for(int here = 1; here < graph.size(); here++){
if(!visited[here]){
dfs(here);
}
}
}
짚고 넘어가야 할 점
백트래킹은 어떤 상황에서 써야 할까?
백트래킹은 주로 임의의 집합에서 주어진 기준대로 원소의 순서를 선택하는 데 사용한다. 검색 공간이 여러 개 주어졌을 때, 검색 공간의 배치, 또는 그 순서가 중요한 경우에 사용한다. 예를 들어 N-queen문제처럼 체스판에 배치된 queen들의 패턴이 중요한 경우에 사용할 수 있고, 순열 또는 조합의 경우의 수를 구하는 것처럼 숫자라는 검색 공간을 선택하는 방식을 구할 때도 사용할 수 있다.
하지만 '이러이러한 상황에서 사용한다~'는 것일 뿐, 백트래킹으로 구현하는 게 항상 적절하다는 의미는 아니다. 시간복잡도가 O(M^N)인 백트래킹은 N이나 M이 커지거나, 가지치기가 적게 되는 케이스가 발생하면 시간 초과가 발생할 수 있다. 따라서 '백트래킹이 적절한 알고리즘인가?'를 정확히 알고 싶다면 몬테 카를로 알고리즘(Monte Carlo Algorithm)을 통해 해당 문제에서 사용하기 적절한 알고리즘인지 판단해야 한다.(이론상으론 말이다)
백트래킹과 깊이 우선 탐색(DFS) 비교
백트래킹은 모든 경우의 수를 구해 해를 찾는 문제를 해결하는 방법론이다. 효율성을 높이기 위해 가지치기로 일부 경로를 탐색하지 않을 수도 있지만, 해가 될 수 있는 모든 경우를 구한다는 것은 바뀌지 않는다.
반면, 깊이 우선 탐색은 그래프 내 모든 정점을 탐색하기 위한 그래프 탐색 알고리즘이다. 따라서 정점을 탐색하는 순서는 중요하지 않다. 일반적으로 프리오더를 사용한다고 했지만, 인오더나 포스트오더로 순회해도 된다.
간단하게, N개가 주어졌을 때 백트래킹은 순서를 고려하여 모든 경우의 수를 구하기 때문에 N*(N-1)*... 1 = N! 개의 경우가 나오며, 깊이 우선 탐색은 순서를 고려하지 않고 한 번씩 선택하면 되기 때문에 N개의 경우가 나온다.
참고자료
http://computing.or.kr/14572/backtracking%EB%B0%B1%ED%8A%B8%EB%9E%98%ED%82%B9/
'C++ > 알고리즘' 카테고리의 다른 글
| [알고리즘 부록] 트리를 순회하는 방법 3가지(프리오더, 인오더, 포스트오더) (1) | 2024.10.16 |
|---|---|
| [알고리즘] 너비 우선 탐색(BFS)와 dx, dy 테크닉 (0) | 2024.10.14 |
| [알고리즘] 최대공약수(GCD)와 유클리드 호제법(Euclidean algorithm) (0) | 2024.10.12 |
| [알고리즘] 소수 판별법과 에라토스테네스의 체 (3) | 2024.10.11 |
| [알고리즘] parametric search와 lower bound, upper bound (0) | 2024.10.02 |





