나만의 작은 도서관
[알고리즘] 소수 판별법과 에라토스테네스의 체 본문
소수 판별법
소수는 양의 약수를 2개만 가지는 자연수, 즉 1과 자기자신으로만 나누어 떨어지는 자연수를 의미한다(1 제외). 임의의 수 N이 소수인지 판별하기 위해선 2~N-1까지의 수들로 N이 나누어 떨어지지 않는 지 확인하면 된다. 코드로 구현하면 다음과 같다.
// 시간복잡도 O(N)
bool isPrime(int num){
for(int i = 2; i < num; i++){
if(num % i == 0) return false;
}
return true;
}
최적화를 할 수는 없을까?
위 코드는 최적화가 가능하다. 2 이상의 자연수 N에 대해서 N의 약수는 짝이 반드시 존재하고, 짝이 되는 약수 중 작은 쪽에 속하는 약수는 √ N을 초과할 수 없기 때문에 num까지가 아닌 √ N이하의 자연수까지만 루프를 돌면 된다. 따라서 코드에 적용하면 다음과 같다.
// 시간복잡도 O(√N)
bool isPrime(int num){
for(int i = 2; i <= sqrt(num); i++){
if(num % i == 0) return false;
}
return true;
}
N 이하의 모든 소수를 찾고 싶은 경우
위의 코드에 2~N까지 반복하는 for문을 추가하여 구하면 되지만, 이럴 경우 시간복잡도가 O(N* √ N)가 된다. N^2이 아니기 때문에 괜찮을 수도 있지만(실제로 본인도 자주 썼지만 문제 없었다) 에라토스테네스의 체를 이용하여보다 덜 복잡한 시간복잡도를 가진 알고리즘을 짤 수 있다.
에라토스테네스의 체란?
임의의 자연수 N이하의 모든 소수들을 찾는 방법이며, 2~N까지의 자연수들을 나열해놓고 지워지지 않은 수 중 가장 작은 수(이하 p라 부름)를 찾은 다음 p의 배수들을 전부 지워가는 과정을 반복하며 모든 소수들을 찾는다. 시간복잡도는 O(N*log(logN))으로 매우 빠른 속도로 많은 양의 소수들을 찾을 수 있지만, 시작할 때 2~N까지의 자연수들을 전부 저장한다는 점 때문에 공간 복잡도가 높은 편이다.
에라토스테네스의 체 동작방식
1. 2~N까지의 자연수들을 저장한 배열을 준비한다. 예시에서 N은 17이며, 2차원 배열처럼 표현했지만 1차원 배열이다.

2. 지우지 않은 수 중 가장 작은 수 p를 찾는다.
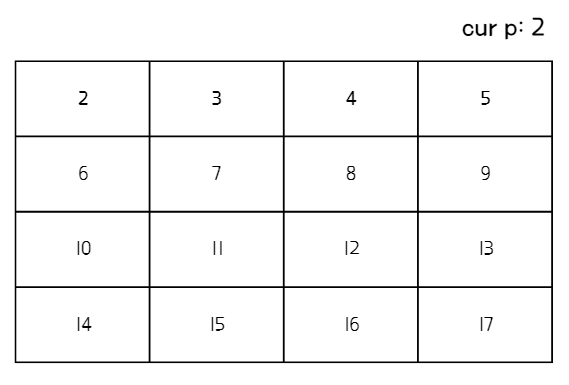
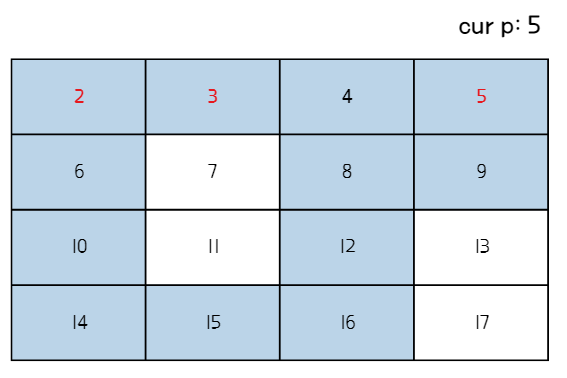
3. p의 배수들을 지운다.(p는 지워도 되고 지우지 않아도 된다)

4. 모든 수가 지워질때까지 2~3번 과정을 반복한다.


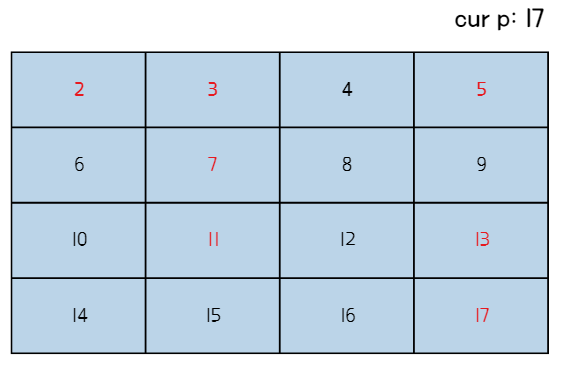
최종 결과(빨간색 숫자가 소수)
구현 코드
// 시간복잡도 O(N*log(logN))
void printPrimeNumbers(int num){
vector<int> arr(num+1);
// 배열을 1부터 시작하는 값으로 채우기
iota(arr.begin(), arr.end(), 1);
for(int i = 2; i <= num; i++){
if(arr[i] == 0) continue;
cout << i << " ";
for(int j = 1; i*j <= num; j++){
arr[i*j] = 0;
}
}
cout << '\n';
}
int main() {
fastio;
printPrimeNumbers(100);
}
// 출력 결과
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
짚고 넘어가야 할 점
에라토스테네스의 체는 왜 시간복잡도가 O(N*log(logN))일까?
시간복잡도가 이렇게 나오는 이유를 알려면 조금 수학적인 이야기를 해야한다. 에라토스테네스의 체 알고리즘은 "소수인 경우에만 배수를 제거"하는 방식이다. 여기서 배수를 제거하는 코드를 보면 알 수 있듯, 한 번 지운 숫자라도 다시 지우는 경우가 있다. 예를 들어, 2와 3의 최소 공배수인 6은 2일 때 0을 대입해 지웠음에도 3일 때 다시 0을 대입하여 지우는 모습을 볼 수 있다. 즉, 앞에서 배수가 지워진 숫자인지 지워지지 않은 숫자인지는 상관없이 현재 소수의 배수라면 지우는 작업을 실행한다. 따라서, 각 소수 p가 배수를 제거할 때 반복하는 횟수는 n/p이며, 이를 식으로 나타내면 아래와 같다.
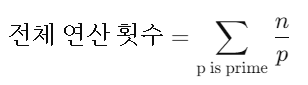
1/2 + 1/3 + 1/4 + ... 와 같이 자연수의 역수들의 합을 조화급수라고 부른다. 위에서 얻은 소수들의 합에 대한 식은 조화급수의 모습을 가지고 있는 것들 볼 수 있다. 조화급수의 근삿값은 lnN + r이므로 값이 n*(lnN + r)일까 싶지만 "소수인 경우에만"을 고려하지 않았기 때문에 그렇지 않아 이 부분을 고려해야한다.
소수 정리(Prime Number Theorem)에 따르면 충분히 큰 N에 대하여 N이하의 소수 개수는 n/logN에 근사하며, 다르게 표현하면 1/logN의 밀도로 소수가 분포되어 있다고 볼 수 있다. 이러한 사실과 적분근사를 활용하면 아래와 같이 근사한 식을 유도할 수 있다. 대충 소수들의 평균적인 분포를 1/logx로 근사했다고 보면된다.
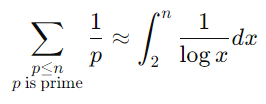
이제 적분을 하면 된다. 1/x을 적분한 함수는 lnx이므로, ln(logN) - ln(2)가 되며 여기에 미리 빼두었던 n을 곱해준 n*( ln(logN) - ln(2))이 전체 연산 횟수가 된다. 이제 이걸 시간복잡도 방식으로 표현하면 O(N*log(logN))이므로, 에라토스테네스의 체의 시간복잡도가 O(N*log(logN))인 것을 알 수 있다.
참고자료
https://www.youtube.com/watch?v=5ypkoEgFdH8
https://pkjung.tistory.com/173
'C++ > 알고리즘' 카테고리의 다른 글
| [알고리즘] 너비 우선 탐색(BFS)와 dx, dy 테크닉 (0) | 2024.10.14 |
|---|---|
| [알고리즘] 백트래킹(backtracking)과 깊이 우선 탐색(DFS) (0) | 2024.10.13 |
| [알고리즘] 최대공약수(GCD)와 유클리드 호제법(Euclidean algorithm) (0) | 2024.10.12 |
| [알고리즘] parametric search와 lower bound, upper bound (0) | 2024.10.02 |
| [알고리즘] 이진 탐색(Binary search) (1) | 2024.03.24 |




