나만의 작은 도서관
[알고리즘] 이진 탐색(Binary search) 본문
이진 탐색이란?
이진 탐색은 정렬된 일련의 값들에서 찾고자 하는 값을 중앙값과 비교한 다음, 비교 결과에 따라 탐색 범위를 중앙값 왼쪽 범위 또는 오른쪽 범위로 줄이며 값을 찾아가는 방식을 의미한다. 매 반복마다 탐색 범위가 절반씩 줄어들기 때문에 시간복잡도는 O(logN)으로 속도가 매우 빠르다는 장점이 있지만 정렬되어 있어야한다는 제약조건이 있다.
동작방식
이진 탐색을 구현하는 방법은 구현한 사람의 스타일에 따라 조금씩 달라진다. 아래의 동작방식은 내가 사용하기 편한 방법을 토대로 설명한 방식이다.(설명은 오름차순으로 정렬된 배열을 기준으로 한다.)
1. 초기화

시작은 위 그림같이 start는 배열의 첫번째 위치, end는 배열의 마지막 위치 + 1로 초기화한다.
2. 범위 나누기
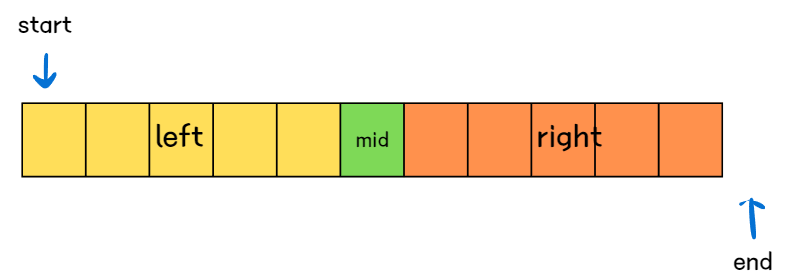
초기화 이후 탐색을 시작한다. 탐색 범위는 [start , end)가 되며, 탐색 범위의 중앙값을 기준으로 왼쪽, 오른쪽 범위로 나누어진다.
3. 대소비교 및 범위 변경
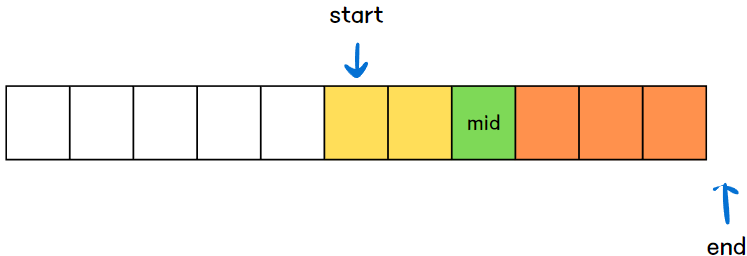

타겟값과 중앙값을 대소비교한다. 만약 타겟값이 중앙값보다 크다면, 중앙값보다 큰 수들이 존재하는 범위에서 찾아야하므로 탐색 범위를 오른쪽으로 변경한다. 반대로 타겟값이 중앙값보다 작으면, 중앙값보다 작은 수들이 존재하는 범위에서 찾아야하므로 탐색 범위를 왼쪽으로 변경한다.
탐색 범위를 변경했다면, 변경된 탐색 범위의 중앙값과 타겟값을 대소비교하는 작업을 반복한다.
4. 탐색 결과 반환


루프를 도는 동안 값을 찾았다면 해당 값의 index를 반환한다.(여기서 주의해야 할 점은 배열에 타겟값과 동일한 값이 여러 개일 경우, 다른 알고리즘을 사용했을 때와 다른 index를 반환할 수 있다. 따라서, 이러한 경우는 lower bound, upper bound를 사용해야한다) 만약, 값의 존재 여부만 알고 싶다면 true나 1같은 리턴값으로 변경하면된다.
반대로 루프를 도는 동안 값을 찾지 못했다면 -1을 반환한다. 필요에 따라 false나 0을 반환해도 상관없다.
구현 코드
int binarySearch(vector<int> &v, int target)
{
int start = 0, end = v.size();
while (start < end) // 탐색 범위(len)의 길이가 1이상인 경우 진입
{
int mid = (start + end) / 2;
if (v[mid] == target)
return mid;
else if (v[mid] < target) // 오른쪽 범위로 줄여야 하는 경우(중앙값 < 타겟값)
start = mid + 1;
else // 왼쪽 범위로 줄여야 하는 경우(중앙값 > 타겟값)
end = mid;
}
return -1;
}
STL로 구현되어 있다.
C++ STL에 binary_search라는 이름으로 함수가 구현되어 있다. <algorithm>헤더에 포함되어 있으며, 리턴 값이 bool타입이라 값을 찾았을 때 값의 index 위치까지 알 수는 없다.
template <class ForwardIterator, class T>
bool binary_search (ForwardIterator first, ForwardIterator last, const T& val)
binary_search(v.begin(), v.end(), value);
짚고 넘어가야 할 점
end의 의미
내가 사용하는 이진 탐색에서 end는 항상 탐색 범위를 1만큼 벗어나 있다. 초기화 할 때도 v.size()로 설정하고, while문 루프 내에서도 탐색 범위 마지막 위치 +1의 자리를 고수하고 있다. 이렇게 end가 항상 1만큼 벗어난 이유는 end를 탐색 범위 마지막 위치의 의미로 사용하는 것이 아닌, v1.end() - v1.begin() = v1.size()처럼 end - start = len이 되도록 사용하는 것이다. 이렇게 하면 while 조건문인 start < end 또한 '탐색 범위의 길이가 1 이상인 경우에만 반복한다' 라는 의미가 된다는 점과 정답 위치를 고려할 때 start 위치만 신경쓰면 된다는 점 때문에 코드 흐름을 이해하기 편해졌다.
mid값을 구할 때 발생한 소수점은 버린다 -> 왼쪽 위치 선택
mid = (start + end) / 2로 mid를 구할 때, 나누기 2로 인해 소수점이 발생할 수 있다. 1번 위치 2번 위치 등 위치 번호는 소수점이 있으면 안되기 때문에 소수점이 발생했을 때 내림, 올림 중 하나를 선택해야한다. 어느 것은 선택해도 이진 탐색을 구현할 수 있지만 start의 위치가 mid 위치가 된다는 점, 정수 타입에서 소수점이 발생했을 때 자동으로 버린다는 점을 이유로 내림을 선택했다.
오른쪽 범위로 줄일 때는 start = mid + 1인데 왼쪽 범위로 줄일 때는 end = mid - 1이 아닌 이유
위 코드는 end가 절대로 답이 되는 위치에 있을 수 없다는 전제로 짰다. 그런데 end = mid - 1을 해서 오른쪽 때와 똑같이 비교한 위치를 제외하여 줄여버리면 end가 답이 되는 위치에 있을 수 있게된다. 이렇게 전제를 무시하게 되면 코드는 무한 루프를 돌거나 잘못된 답을 내릴 수 있기 때문에 답이 될 가능성이 있는 mid - 1이 아닌, 절대로 답이 될 수 없는 mid값을 end에 대입하는 것이다.
참고자료
'C++ > 알고리즘' 카테고리의 다른 글
| [알고리즘] 너비 우선 탐색(BFS)와 dx, dy 테크닉 (0) | 2024.10.14 |
|---|---|
| [알고리즘] 백트래킹(backtracking)과 깊이 우선 탐색(DFS) (0) | 2024.10.13 |
| [알고리즘] 최대공약수(GCD)와 유클리드 호제법(Euclidean algorithm) (0) | 2024.10.12 |
| [알고리즘] 소수 판별법과 에라토스테네스의 체 (4) | 2024.10.11 |
| [알고리즘] parametric search와 lower bound, upper bound (0) | 2024.10.02 |




