나만의 작은 도서관
[알고리즘] 프림 알고리즘(Prim Algorithm), 크루스칼 알고리즘(Kruskal Algorithm) 본문
프림 알고리즘(Prim Algorithm)과 크루스칼 알고리즘이란(Kruskal Algorithm)?
프림 알고리즘과 크루스칼 알고리즘은 그래프에서 최소신장트리(Minimum Spanning Tree, 줄여서 MST라고 부름)를 찾는 알고리즘이다. 이 두 알고리즘 모두 "부분적으로 최적인 고려사항에 따라 간선을 선택"하기 때문에 그리디 알고리즘(Greedy Algorithm)으로 분류된다.
최소신장트리란?
최소신장트리는 그래프의 모든 정점을 포함하는 트리들 중 가중치의 합이 최소인 트리를 말한다. 주로 가장 적은 비용으로 모든 지점을 연결하고 싶을 때 사용한다.
동작방식(프림 알고리즘)

1. 초기화
시작점을 선택한다. 시작점은 어떤 정점을 선택해도 상관없지만, 아래 예시에서는 편의상 1번 정점을 선택한다.
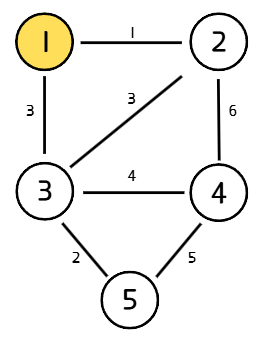
2. 간선 추가
MST를 구하기 위해 선택한 간선들의 집합을 F라고 했을 때, F로 연결된 정점과 그렇지 않은 정점을 연결하는 간선 중 가장 가중치가 작은 간선을 선택하여 F에 추가한다.
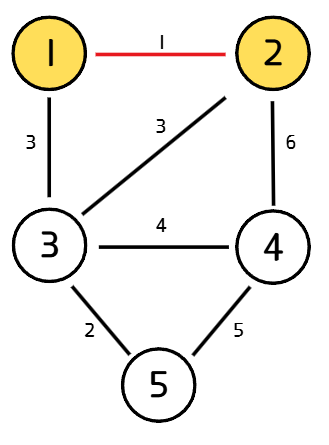
3. 반복
2번 과정을 V-1번 반복한다.



4. 최종 결과
반복을 마치면 F를 통해 MST를 얻을 수 있다.

동작방식(크루스칼 알고리즘)

1. 초기화
그래프에 존재하는 모든 간선들을 가중치가 작은 순으로 정렬한다. 그리고 각 정점에 대해 서로소 부분 집합을 구축한다.
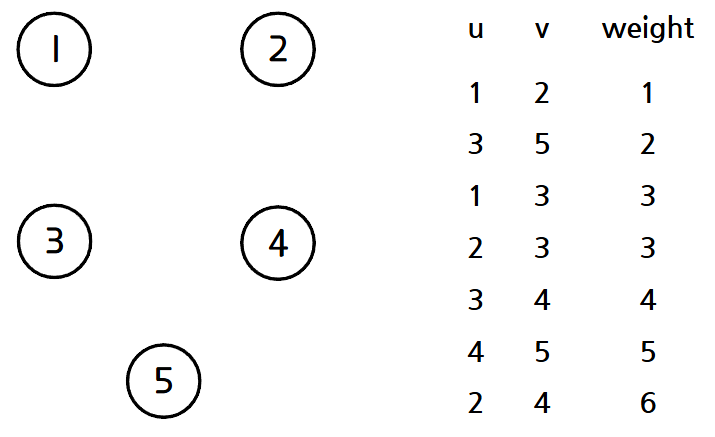
2. 간선 선택
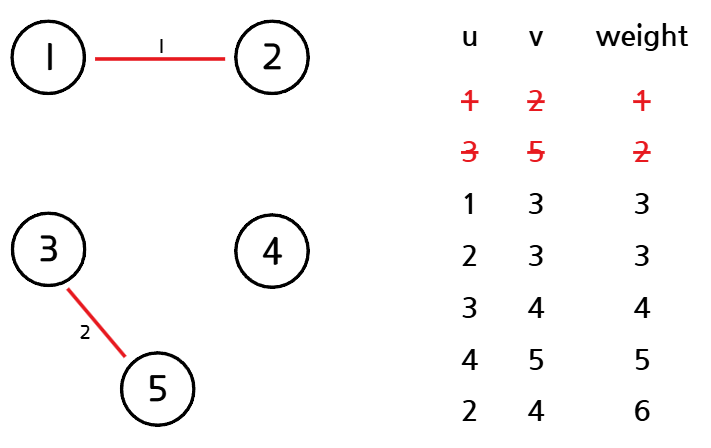
가중치가 가장 작은 간선을 선택한다. 선택한 간선이 정점 u, v를 연결하는 간선이라고 할 때, u, v가 같은 집합에 속해있다면(사이클을 만든다면) 해당 간선을 버리고 2번 과정을 반복한다.
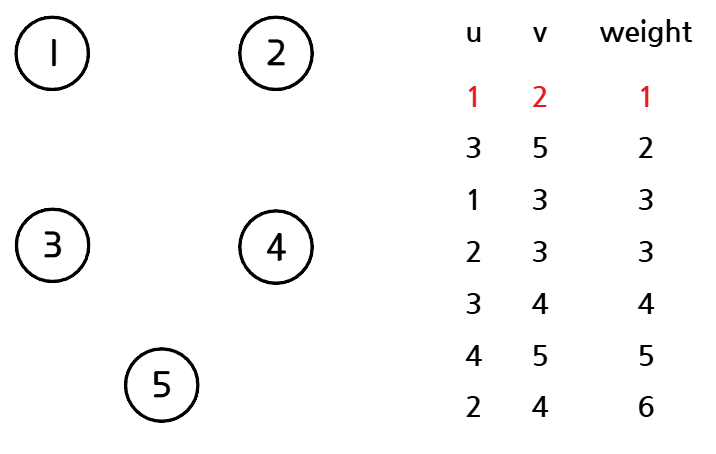
3. 간선 추가 및 집합 병합
MST를 구하기 위해 선택한 간선들의 집합을 F라고 했을 때, 선택한 간선을 F에 추가하고, u가 속한 집합과 v가 속한 집합을 하나로 합친다.

4. 반복
2~3번 과정을 V-1번 반복한다.
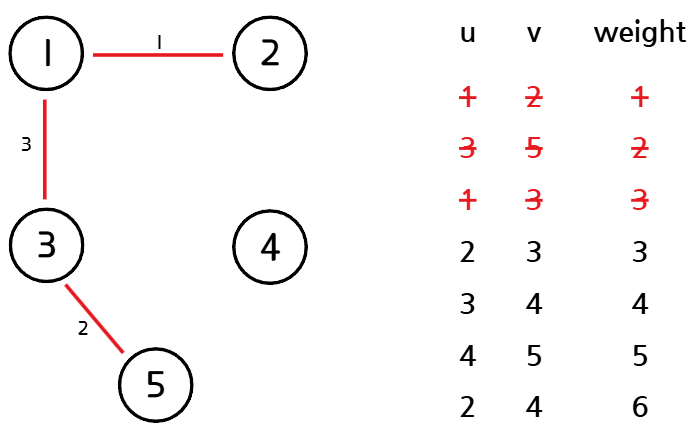

5. 최종 결과
반복을 마치면 F를 통해 MST를 얻을 수 있다.

구현 코드
프림 알고리즘
아래 코드에 구현된 프림 알고리즘은 V-1개의 간선을 찾기 위해 최대 E번 반복할 수 있고 매 반복마다 우선순위 큐에서 데이터를 추출한다. 따라서 시간복잡도는 O(ElogE)이다. (logE는 logV와 근사하므로 O(ElogV)로 표현할 수도 있다)
int v, e;
vector<vector<pair<int, int>>> adj;
// 시간복잡도 O(ElogE)
int prim(){
vector<bool> visited; visited.resize(v+1);
int cnt = 0;
int ans = 0;
int start = 1;
// tuple<int, int, int> : {가중치, 정점 1, 정점 2}
priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<tuple<int, int, int>>> pq;
visited[start] = true;
for(auto ed : adj[start]){
pq.push({ed.first, start, ed.second});
}
while(cnt < v - 1){
int weight, vtx1, vtx2;
tie(weight, vtx1, vtx2) = pq.top(); pq.pop();
// 이미 방문한 정점이면 넘어간다.
if(visited[vtx2]) continue;
visited[vtx2] = true;
cnt++;
ans += weight;
// 인접한 간선들을 우선순위 큐에 삽입한다.
for(auto ed : adj[vtx2]){
pq.push({ed.first, vtx2, ed.second});
}
}
return ans;
}
크루스칼 알고리즘
아래 코드에 구현된 프림 알고리즘은 정렬을 하는데 O(ElogE), union-find알고리즘을 최대 E번 반복하여 O(ElogE), 서로소 집합을 초기화하는데 O(E)만큼의 시간이 걸린다. 따라서, min( ElogE , ElogE, E) = ElogE이다. 따라서 시간복잡도는 O(ElogE)이다. (크루스칼 알고리즘 또한 logE는 logV와 근사하므로 O(ElogV)로 표현할 수도 있다)
vector<int> parent;
// union-find 알고리즘(경로 압축 + union by rank포함)
int find(int x){
if(parent[x] < 0) return x;
return parent[x] = find(parent[x]);
}
bool is_diff_group(int u, int v){
u = find(u);
v = find(v);
if(u == v) return false;
if(parent[u] == parent[v]) parent[u]--;
if(parent[u] < parent[v]) parent[v] = u;
else parent[u] = v;
return true;
}
vector<tuple<int, int, int>> edge; // tuple<int, int, int> : {가중치, 정점 1, 정점 2}
// 시간복잡도 O(ElogE)
int kruskal(){
int cnt = 0;
int ans = 0;
// init
sort(edge.begin(), edge.end()); // 간선을 가중치가 짧은 순으로 정렬
fill(parent.begin(), parent.end(), -1); // 부모 정점 초기화
for(int i = 0; i < e; i++){
int vtx1, vtx2, weight;
tie(weight, vtx1, vtx2) = edge[i];
// 간선의 시작점과 끝점이 같은 집합이라면(사이클을 만듦) 넘어간다.
if(!is_diff_group(vtx1, vtx2)) continue;
cnt++;
ans += weight;
// v-1개의 간선을 모두 찾으면 미리 루프탈출
if(cnt == v-1) break;
}
return ans;
}
짚고 넘어가야 할 점
프림 알고리즘, 크루스칼 알고리즘이 V-1번 반복하는 이유
프림 알고리즘이랑 크루스칼 알고리즘이 V-1번 반복하는 이유는 매 반복마다 하나의 간선을 추가하며 MST는 V-1개의 간선으로 이루어져 있기 때문이다.
두 알고리즘이 항상 MST를 반환한다 보장할 수 있는 이유(증명)
프림 알고리즘
G(V, E)를 연결된 가중치가 있는 비방향 그래프, F는 MST가 되는데 유망한 E의 부분집합, e는 F에 추가되어도 사이클을 만들지 않는 간선이라고 가정하자.
프림 알고리즘이 항상 MST를 만들어 낸다는 것을 증명하고 싶다면 매 반복마다 F에 e를 추가해도 F가 유망한지 증명하면 된다.
F ∪ {e}가 유망한가?
F가 유망하다면 F ⊆ F'을 만족하는 F'이 반드시 존재하며, 모든 정점을 F'에 포함된 간선만으로 연결한 G(V, F')는 MST이다.
1) F'에 e가 포함되어 있는 경우
만약 F'에 e가 포함되어 있다면, 다음 관계가 성립된다.
F ∪ {e} ⊆ F'
이는 F ∪ {e}가 유망하다는 것을 의미하고, 따라서 증명되었다.
2) F'에 e가 포함되어 있지 않은 경우

만약 F'에 e가 포함되어 있지 않다면, F' ∪ {e}에는 정확히 하나의 사이클이 반드시 존재하게 된다. F에 포함된 간선에 연결된 정점들을 Y라고 했을 때 F' ∪ {e}에서 발생한 사이클은 간선 e와 Y에서 V-Y로 연결하는 또 다른 간선 e'를 반드시 포함하게된다. 여기서 e'을 제거하면 사이클이 제거되고 다시 신장트리가 되는데, 간선 e는 Y에서 V-Y로 연결하는 모든 간선 중 가장 가중치가 작으므로(프림 알고리즘의 동작방식), e의 가중치는 e'보다 항상 작거나 같다. 따라서 다음은 MST가 된다.
F' ∪ {e} - {e'}
결론적으로 e'은 F에 절대로 속할 수 없으므로 F는 F' ∪ {e} - {e'}의 모습을 한 MST에 대해 유망하다.
따라서 F ∪ {e}는 모든 상황에서 유망하며, 프림 알고리즘은 항상 MST를 만들어 낸다.
크루스칼 알고리즘
G(V, E)를 연결된 가중치가 있는 비방향 그래프, F는 MST가 되는데 유망한 E의 부분집합, e는 F에 추가되어도 사이클을 만들지 않는 간선이라고 가정하자.
크루스칼 알고리즘이 항상 MST를 만들어 낸다는 것을 증명하고 싶다면 프림 알고리즘과 동일하게 매 반복마다 F에 e를 추가해도 F가 유망한지 증명하면 된다.
F ∪ {e}가 유망한가?
F가 유망하다면 F ⊆ F'을 만족하는 F'이 반드시 존재하며, 모든 정점을 F'에 포함된 간선만으로 연결한 G(V, F')는 MST이다.
1) F'에 e가 포함되어 있는 경우
만약 F'에 e가 포함되어 있다면, 다음 관계가 성립된다.
F ∪ {e} ⊆ F'
이는 F ∪ {e}가 유망하다는 것을 의미하고, 따라서 증명되었다.
2) F'에 e가 포함되어 있지 않은 경우
만약 F'에 e가 포함되어 있지 않다면, F' ∪ {e}에는 정확히 하나의 사이클이 반드시 존재하게 되며 해당 사이클에는 e를 반드시 포함하고 있다. 그런데 F ∪ {e}는 사이클이 존재하지 않으므로 사이클에 속한 어떤 간선 e'이 E-F에 존재해야만 한다. F ∪ {e'}는 F'의 부분집합이므로 사이클이 존재하지 않는다. 이는 크루스칼 알고리즘이 e와 e'을 둘 중 하나를 선택할 수 있었음에도 e를 선택했다고 할 수 있다. 그러므로 e의 가중치는 e'의 가중치보다 크지 않다. F' ∪ {e}에서 e를 제거하면 사이클이 제거되고 다시 신장트리가 되는데, 해당 신장트리를 표현하는 다음 집합은 MST가 된다.
F' ∪ {e} - {e'}
따라서 F ∪ {e}는 모든 상황에서 유망하며, 크루스칼 알고리즘은 항상 MST를 만들어 낸다.
프림 알고리즘 vs 크루스칼 알고리즘
프림 알고리즘과 크루스칼 알고리즘은 목적도 똑같고, 시간복잡도도 동일하다.(엄밀히 말하면 그래프의 밀도에 따라 조금 다르다) 그렇기 때문에 뭘 써도 상관 없지만, union-find 알고리즘을 이해하고 있는 입잡에선 크루스칼 알고리즘이 구현하기 쉽기 때문에 크루스칼 알고리즘을 사용하는 것을 선호한다.
참고자료
책
알고리즘 기초 - Richard E. Neapolitan
영상
'C++ > 알고리즘' 카테고리의 다른 글
| [알고리즘] CCW(Counter ClockWise)와 선분 교차 판정 (1) | 2024.10.30 |
|---|---|
| [알고리즘] Union-Find 알고리즘 (0) | 2024.10.29 |
| [알고리즘] A* 알고리즘(A star algorithm) (0) | 2024.10.24 |
| [알고리즘] 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2024.10.23 |
| [알고리즘] 다익스트라 알고리즘(Dijkstra Algorithm) (2) | 2024.10.19 |




