나만의 작은 도서관
[알고리즘] 다익스트라 알고리즘(Dijkstra Algorithm) 본문
다익스트라 알고리즘(Dijkstra Algorithm)이란?
다익스트라 알고리즘은 가중치가 있는 그래프(weighted graph)중 음수 가중치가 없는 그래프에서 시작점을 기준으로 다른 모든 정점으로 가는 최단 거리를 구하는 알고리즘이다. 다익스트라 알고리즘은 최단 거리를 구하는 매 단계에서 가장 짧은 경로만 선택하기 때문에 그리디 알고리즘(greedy algorithm)으로 분류 된다.
동작방식

1. 초기화
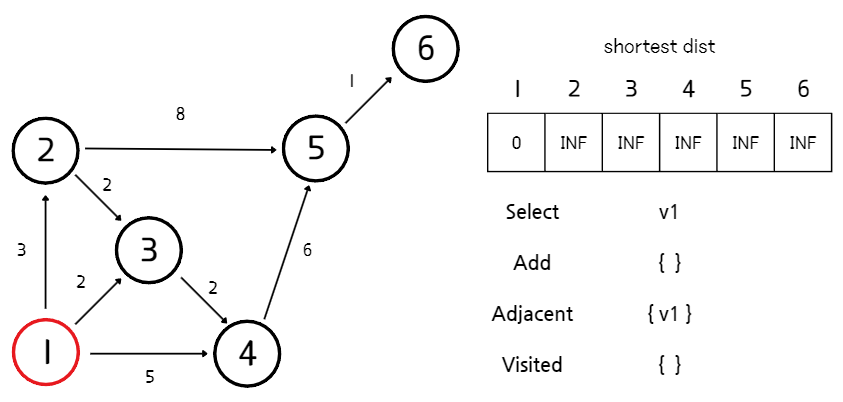
- 시작점에서 각 정점으로 가는 최단 거리를 저장할 배열을 생성한다. 배열은 시작점과의 거리를 0으로, 다른 정점들과의 거리는 무한대(INF)로 초기화한다. (편의상 시작점은 v1로 설정하였다.)
- 아래 그림에서 Select, Add, Adjacent, Visited는 다음과 같은 의미를 가진다.
- Select: 현재 단계에서 선택한 정점
- Add: 추가된 인접한 정점들의 집합
- Adjacent: 방문한 정점들을 거쳐 도달할 수 있는 정점들의 집합.
- Visited: 방문한 정점들의 집합. 방문한 정점들은 최단 거리가 확정된 정점을 의미한다.

2. 방문할 정점 선택
- 방문한 정점들을 거쳐 도달할 수 있는 정점들의 집합 (Adjacent)에서 시작점으로부터 가장 짧은 경로를 가진 정점을 선택한다. 처음에는 시작점이 선택된다.
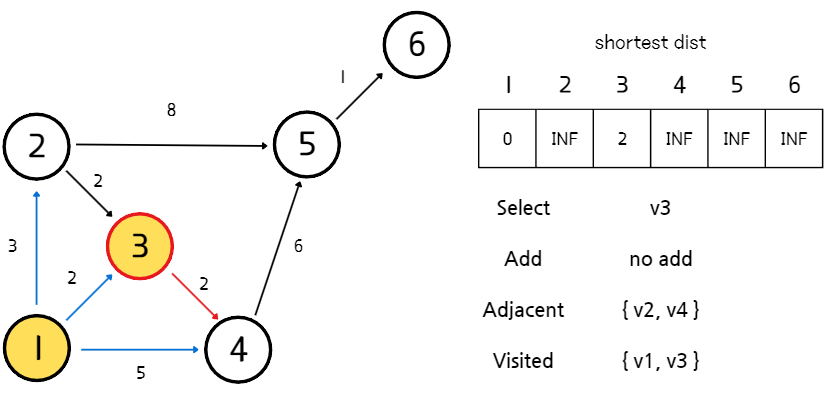
3. 방문 처리
- 선택한 정점을 방문 처리하고(Visited에 추가), 선택한 정점과의 경로는 최단 경로임으로 해당 경로의 길이를 배열에 저장한다. 이후, 선택한 정점과 연결된 정점들을 탐색하여 도달할 수 있는 새로운 정점들을 인접 집합(Adjacent)에 추가한다.

4. 2~3번 과정을 반복
- 모든 정점으로 가는 최단 거리를 구할 때까지(또는 방문할 때까지) 2~3 과정을 반복한다.



5. 최종 결과
- 최종적으로 각 정점으로 가는 최단 거리를 저장하고 있는 배열이 된다.

구현 코드
다익스트라 알고리즘을 구현하는 방법은 여러 가지 있지만, 방문할 정점을 선택하는 과정에서 차이가 난다. 해당 과정을 어떻게 구현하느냐에 따라 시간복잡도가 크게 달라지며, 아래에선 총 3가지의 방법을 설명해 두었다.
첫 번째 방법: 시간복잡도 O(VE)
첫 번째 방법은 1) 최단 거리가 확정된 정점들의 모든 간선들을 확인하여 2) 가장 짧은 거리로 도달하는 정점을 방문할 정점으로 선택하는 과정을 3) 방문 가능한 모든 정점들의 최단 거리를 찾을 때까지 반복하는 방법이다. 시간복잡도는 매 반복마다 정점을 선택할 때 방문한 모든 간선을 확인하므로 최대 E번, 반복은 V-1번(시작점을 제외한 모든 정점)함으로 O(VE)가 된다. (E는 최대 1 + 2 +... + V-1 = V(V-1) / 2개 이므로, 시간복잡도를 V로 통일하면 O(V^3)이 된다.) 코드는 아래와 같다.
int V, E, K;
vector<vector<pair<int, int>>> graph; // first : vtx, second: weight
// 시간복잡도 O(VE)
vector<int> dijkstra1(int start){
vector<int> shortest_dist(V+1, INF);
// init
shortest_dist[start] = 0;
// O(V)
for(int i = 0; i < V-1; i++){
int minDist = INF;
int selected_vtx = -1;
// 확정된 정점들로부터 뻗어나가는 모든 간선 체크 O(E)
for(int vtx = 1; vtx <= V; vtx++){
// 아직 확정되지 않은 정점이라면 패스
if(shortest_dist[vtx] == INF) continue;
for(pair<int, int> ed : graph[vtx]){
// 도착한 정점이 확정된 정점이면 패스
if(shortest_dist[ed.first] != INF) continue;
if(shortest_dist[vtx] + ed.second < minDist){
minDist = shortest_dist[vtx] + ed.second;
selected_vtx = ed.first;
}
}
}
// 더 이상 선택할 수 있는 정점이 없는 경우
if(selected_vtx == -1) break;
// 선택된 정점을 확정셋에 추가
shortest_dist[selected_vtx] = minDist;
}
return shortest_dist;
}
두 번째 방법: 시간복잡도 O(V^2 + E)
두 번째 방법은 이전 단계의 최단 경로 배열에서 가장 짧은 경로를 만들어낸 후보 정점(방문하지 않은 인접 정점)을 방문할 정점으로 선택하는 방법이다. 이 방법은 1) 매 반복마다 최단 경로 배열을 순회하여 후보 정점을 찾고(V번), 2) 찾은 후보 정점의 모든 간선을 순회하며(총 합 E번), 3) 반복은 방문 가능한 모든 정점의 최단 경로를 구할 때까지 반복하므로(최대 V-1번) 시간복잡도는 O(V^2 + E)가 된다. 코드는 아래와 같다.
int V, E, K;
vector<vector<pair<int, int>>> graph; // first : vtx, second: weight
// 시간복잡도 O(V^2+E)
vector<int> dijkstra2(int start){
vector<int> shortest_dist(V+1, INF);
vector<bool> visited(V+1);
// init
shortest_dist[start] = 0;
visited[start] = true;
// 시작점과 인접한 정점들의 최단거리를 갱신.
for(const pair<int, int>& ed : graph[start]){
int vtx = ed.first;
int weight = ed.second;
// 여러 개의 간선이 같은 인접 정점과 연결되어 있을때도 최단거리를 유지하기 위해 min추가.
shortest_dist[vtx] = min(shortest_dist[vtx], shortest_dist[start] + weight);
}
// 시작점을 제외한 모든 정점들을 선택할 때까지 반복 O(V)
for(int i = 0; i < V-1; i++){
int minDist = INF;
int selected_vtx = -1;
// 1. 모든 후보 정점(방문하지 않은 인접 정점)들중 가장 짧은 경로로 도달 가능한 정점을 선택. O(V)
for(int vtx = 1; vtx <= V; vtx++){
if(!visited[vtx] && shortest_dist[vtx] < minDist){
selected_vtx = vtx;
minDist = shortest_dist[vtx];
}
}
// 선택 가능한 정점이 없는 경우 루프 탈출
if(selected_vtx == -1) break;
// 2. 선택한 정점의 최단거리를 확정 및 방문 처리.
shortest_dist[selected_vtx] = minDist;
visited[selected_vtx] = true;
// 3. 선택한 정점과 인접한 정점들의 최단거리를 갱신함으로써 후보 정점을 추가. 총 합 O(E)
for(pair<int, int> ed : graph[selected_vtx]){
shortest_dist[ed.first] = min(shortest_dist[ed.first], shortest_dist[selected_vtx] + ed.second);
}
}
return shortest_dist;
}
세 번째 방법: 시간복잡도 O(ElogV)
세 번째 방법은 <정점 k, 정점 k까지 경로 길이> 쌍으로 된 데이터가 있을 때, 이 데이터들을 경로 길이가 짧은 순으로 정렬하는 우선순위 큐에서 pop 한 데이터가 해당 시점에서 최단 경로일 경우 확장(인접 노드를 순회하면서 최단 경로를 갱신한 경로를 우선순위 큐에 push 하는 과정)하는 방법이다. 핵심 아이디어를 한 마디로 정의하면 아래와 같다.
현재 경로가 최단 경로라면 인접 노드들의 최단 거리를 완화(Relaxation)하고,
완화로 거리가 갱신된 경로는 큐에 push한다.
참고로...
우선순위 큐에서 pop한 데이터의 정점이 이전에 뽑힌 적이 없다면 데이터의 경로 거리는 "해당 정점의 최종 최단 거리"임이 보장된다. 왜냐하면 방문 가능한 모든 정점과 연결된 경로 중 가장 짧은걸 뽑은 결과라 자연스레 같은 정점을 목적지로 한 모든 경로 중에서 가장 짧은 거리임이 보장되기 때문.
시간복잡도 분석
- 최단 경로 선택: 우선순위 큐에서 가장 거리가 짧은 정점을 꺼내는 연산은 정점의 개수(V)만큼 발생한다. 최악의 경우 모든 간선(E)이 들어있는 우선순위 큐에서 데이터를 꺼낼 수 있으므로 시간 복잡도는 O(VlogE) 가 된다.
- 최단 거리 갱신: 정점을 선택하면 선택한 정점과 연결된 간선들을 순회한다. 이때 더 짧은 경로를 발견하면 최단 거리 갱신 및 우선순위 큐에 삽입이 발생하는데, 최악의 경우 모든 간선(E)이 큐에 삽입될 수 있으므로 시간복잡도는 가 된다.
따라서 전체 시간 복잡도는 O(VlogE + ElogE)가 되며, 일반적으로 E >= V이므로 최종적으로 O(ElogV)로 표현된다.
(시간복잡도에서 logE가 아닌 logV로 표현한 이유는 일반적으로 다익스트라 알고리즘의 시간복잡도를 표현할때 logV로 표현하기 때문. 사실 log가 붙은 이상 E든 V든 상관없다) 코드는 아래와 같다.
struct cmp
{
bool operator()(const pair<int, int>& a, const pair<int, int>& b){
return a.second > b.second;
}
};
int V, E, K;
vector<vector<pair<int, int>>> graph; // first : vtx, second: weight
vector<int> dijkstra3(int start){
priority_queue<pair<int, int>, vector<pair<int, int>>, cmp> pq; // first : node_no, second: distance
vector<int> shortest_dist(V+1, INF);
// init
shortest_dist[start] = 0;
pq.push({start, 0});
// path : (vtx, length)
// adj : (vtx, weight)
while(!pq.empty()){
pair<int, int> cur_path = pq.top(); pq.pop();
if(cur_path.second > shortest_dist[cur_path.first]) continue;
for(pair<int, int> adj : graph[cur_path.first]){
int next_vtx = adj.first;
int next_dist = cur_path.second + adj.second;
if(next_dist < shortest_dist[next_vtx]){
shortest_dist[next_vtx] = next_dist;
pq.push({next_vtx, shortest_dist[next_vtx]});
}
}
}
return shortest_dist;
}
최단 경로 추적하기
플로이드 알고리즘과 더불어, 다익스트라 알고리즘 또한 최단 경로를 추적할 수 있다. 다익스트라 알고리즘에서 최단 경로를 추적하려면, 각 정점에 도달하기 직전의 경로 정보를 저장하면된다. 이를 위해 부모(이전) 정점을 저장하는 배열을 추가하고, 최단 경로를 구할 때 이 정보를 이용해 경로를 추적하면 된다. 코드는 아래와 같다.
struct cmp
{
bool operator()(const pair<int, int>& a, const pair<int, int>& b){
return a.second > b.second;
}
};
int V, E, K;
vector<vector<pair<int, int>>> graph; // first : vtx, second: weight
vector<int> parent; // 추가된 코드
vector<int> dijkstra3(int start){
priority_queue<pair<int, int>, vector<pair<int, int>>, cmp> pq; // first : node_no, second: distance
vector<int> shortest_dist(V+1, INF);
// init
shortest_dist[start] = 0;
pq.push({start, 0});
fill(parent.begin(), parent.end(), -1); // 추가된 코드
// path : (vtx, length)
// adj : (vtx, weight)
while(!pq.empty()){
pair<int, int> cur_path = pq.top(); pq.pop();
if(cur_path.second > shortest_dist[cur_path.first]) continue;
for(pair<int, int> adj : graph[cur_path.first]){
int next_vtx = adj.first;
int next_dist = cur_path.second + adj.second;
if(next_dist < shortest_dist[next_vtx]){
shortest_dist[next_vtx] = next_dist;
pq.push({next_vtx, shortest_dist[next_vtx]});
parent[next_vtx] = cur_path.first; // 추가된 코드: 다음 정점의 부모를 현재 정점으로 설정
}
}
}
return shortest_dist;
}
// 최단 경로를 추적하는 함수
void printPath(int dst, const vector<int>& parent) {
vector<int> path;
// 목적지에서 시작 노드로 역추적
for (int v = dst; v != -1; v = parent[v]) {
path.push_back(v);
}
// 경로를 역순으로 만들어 올바른 순서로 반환
reverse(path.begin(), path.end());
for(int vtx : path){
cout << vtx << " ";
}
cout << '\n';
}
짚고 넘어가야 할 점
음수 가중치가 있으면 사용할 수 없는 이유
다익스트라 알고리즘은 그래프에 음수 가중치가 있으면 사용할 수 없다는 제약 조건이 있다. 그 이유는 다익스트라 알고리즘이 "한 번 선택된 정점의 최단 경로는 더 이상 변경되지 않는다"는 가정하에 고안된 알고리즘인데 음수 가중치가 존재하면 이러한 가정이 성립되지 않기 때문이다. 아래 그림을 보면 쉽게 이해할 수 있다.

1번 정점을 시작점으로 선택하고 다익스트라 알고리즘을 사용했을 때, 2번 정점으로 가는 최단 경로는 1->2로 최단 거리는 3이 된다. 하지만 실제 최단 거리는 1 -> 3 -> 2 경로를 통해 얻은 1로, 다익스트라 알고리즘으로 얻은 거리가 최단 거리가 아님을 알 수 있는데, 이는 가중치가 음수를 포함하면서 현재의 최단 거리가 이후에 계산된 거리보다 항상 작다는 것을 보장할 수 없기 때문이다.
참고자료
'C++ > 알고리즘' 카테고리의 다른 글
| [알고리즘] A* 알고리즘(A star algorithm) (0) | 2024.10.24 |
|---|---|
| [알고리즘] 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2024.10.23 |
| [알고리즘] 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm) (0) | 2024.10.16 |
| [알고리즘 부록] 트리를 순회하는 방법 3가지(프리오더, 인오더, 포스트오더) (1) | 2024.10.16 |
| [알고리즘] 너비 우선 탐색(BFS)와 dx, dy 테크닉 (0) | 2024.10.14 |




