나만의 작은 도서관
[알고리즘] CCW(Counter ClockWise)와 선분 교차 판정 본문
CCW(Counter ClockWise)란?
CCW(Counter ClockWise) 알고리즘은 평면 위에 놓인 세 점의 방향을 계산하여 이 점들이 시계 방향인지, 반시계 방향인지, 혹은 일직선 상에 있는지 확인하는 데 사용한다. 예를 들어 세 점 A, B, C가 주어졌을 때 구하고자 하는 방향이 A -> B -> C라면, 벡터 AB와 벡터 BC을 이용해 방향을 계산하는 방식이다. CCW 알고리즘은 기하학 알고리즘(geometry algorithm)으로 분류되며 볼록 껍질(Convex Hull), 선분 교차 판정과 같은 문제에서 활용할 수 있다.
CCW 공식과 방향 판별법
세 점 A(x1, y1), B(x2, y2), C(x3, y3)가 주어졌을 때, A -> B -> C의 방향은 다음과 같은 식을 사용하여 계산한다.
CCW(A, B, C) = (x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1)
계산한 CCW(A, B, C)값의 의미는 다음과 같다.
- CCW(A, B, C) < 0: A -> B -> C의 방향은 반시계 방향이다.
- CCW(A, B, C) > 0: A -> B -> C의 방향은 시계 방향이다.
- CCW(A, B, C) = 0: A, B, C는 일직선 상에 있다.

왜 위와 같은 식이 유도되는가?

2개의 벡터는 하나의 평면을 결정하며, 두 벡터를 외적한 결과는 법선 벡터(평면에 수직인 벡터)이다. 이 법선 벡터를 h라고 했을 때 h의 z값은 오른손의 법칙에 의해 두 벡터가 시계 방향이면 양수, 반시계 방향이면 음수가 된다. 따라서 두 벡터의 법선 벡터를 구할 수 있다면 z값을 통해 평면을 결정한 두 벡터가 시계 방향이었는지, 반시계 방향이었는지 알 수 있다.
외적 공식
두 벡터를 각각 u, v라고 할 때 u x v는 u와 v를 외적한다는 의미를 가진다. u = (m1, m2, m3), v = (n1, n2, n3)라고 할 때, u x v는 다음과 같다.

적용하기
위 식을 통해 법선 벡터 h의 z값은 m1m2 - m2n1라는 것을 알 수 있다. 여기서 u를 벡터 AB로, v를 벡터 CD로 치환했을 때 m1m2 - m2n1를 다음과 같이 표현할 수 있다.
A(x1, y1), B(x2, y2), C(x3, y3)일 때
m1*m2 - m2*n1 = (x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1)
따라서 CCW(A, B, C) = (x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1)이 되며, 이 값을 통해 세 점의 방향을 구할 수 있다.
구현 코드(CCW)
#define point pair<long long, long long>
int ccw(point A, point B, point C) {
long long res = (B.first - A.first)*(C.second - A.second) - (C.first - A.first)*(B.second - A.second);
return (res > 0) - (res < 0); // -1, 0, 1 반환
}
선분 교차 판정이란?
선분 교차 판정은 두 선분이 주어졌을 때 선분들이 서로 교차하는지 판정하는 문제이다. 선분 교차 문제를 푸는 방법은 다양하지만 CCW를 활용하면 보다 간단하고 효율적이게 문제를 해결할 수 있다. CCW를 이용해 선분 교차 판정을 하는 법은 다음과 같다.
isCross(AB, CD) = CCW(A, B, C)*CCW(A, B, D) <= 0 && CCW(C, D, A)*CCW(C, D, A)
(단, 둘 다 0인 경우 min(C, D) <= max(A, B) && min(A, B) <= max(C, D) )
왜 위와 같은 식이 유도되는가?
1. CCW*CCW의 의미

선분 AB와 선분 CD가 주어졌을 때, CCW(A, B, C)와 CCW(A, B, D)는 선분 AB를 연장시킨 직선을 l1 기준으로 점 C, D가 어느 영역에 있는지 알 수 있다. CCW(A, B, C)를 예로 들자면 다음과 같다. (음수는 -1, 양수는 1로 표현)
- CCW(A, B, C) = -1 : 점 C는 반시계 영역에 있다
- CCW(A, B, C) = 1 : 점 C는 시계 영역에 있다
- CCW(A, B, C) = 0 : 점 C는 l1 위에 있다.
같은 방식으로 CCW(A, B, D)의 값을 구하여 CCW(A, B, C)*CCW(A, B, D)의 값에 따라 새로운 결과를 도출해 낼 수 있는데, 의미는 다음과 같다.
- CCW(A, B, C)*CCW(A, B, D) = -1 : 두 CCW의 방향이 서로 다르다. 따라서, 점 C와 D는 서로 다른 영역에 있다.
- CCW(A, B, C)*CCW(A, B, D) = 1 : 두 CCW의 방향이 같다. 따라서, 점 C와 D는 같은 영역에 있다.
- CCW(A, B, C)*CCW(A, B, D) = 0 : 점 C와 D 중적어도 하나는 l1 위에 존재한다.
따라서 CCW(A, B, C)*CCW(A, B, D)의 값을 통해 l1을 기준으로 점 C와 D의 위치관계를 알 수 있다.
2. 일반적인 경우('X'자 모양 교차)
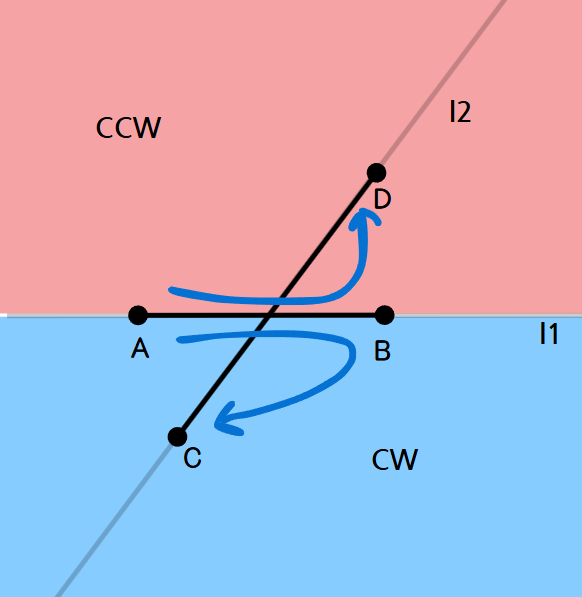
위 그림을 예시로 들어보자. 위 그림에서 CCW(A, B, C)를 구하면 1(시계 방향), CCW(A, B, D)를 구하면 -1 (반시계 방향) 이 나오므로 곱한 값은 -1이 나온다. -1이라는 결과를 통해 점 C와 D는 서로 다른 영역에 존재한다는 것을 알 수 있는데, 두 점이 서로 다른 영역에 존재한다는 것은 선분 CD가 반드시 l1을 관통한다는 의미로 해석할 수 있으며, 이는 l1과 선분 CD는 교차한다는 의미로도 해석할 수 있다.
따라서, CCW의 결과값이 -1이라면, l1과 선분 CD는 교차한다

하지만 l1과 교차할 뿐, 구하고자 하는 선분 AB와의 교차가 아니므로 CCW(A, B, C)*CCW(A, B, D)의 값이 -1이 나와도 두 선분이 교차하지 않을 수 있다. 따라서 두 선분이 반드시 교차하는 경우를 구하고 싶다면 CCW(C, D, A)*CCW(C, D, B)의 값 또한 -1이 나오는지 확인해야 한다.
그렇다면 두 CCW의 결과값이 -1이 나오는 지만 확인하면 될까? 안타깝게도 결과값이 -1이 나오는 경우에만 교차하지는 않는다. 모든 교차를 구하기 위해선 예외적인 상황들에 대한 처리를 해야 한다. 예외적인 상황들은 1) 세 점이 일직선 상에 있는 경우, 2) 네 점이 일직선 상에 있는 경우가 있다.
3. 세 점이 일직선 상에 있는 경우

세 점이 일직선 상에 있는 경우는 총 3가지 경우가 존재한다. 이 중 교차하지 않는 경우는 한 가지 경우밖에 없는데(위 그림에서 3번), 교차하지 않는 경우에만 결괏값이 1이 나오는 것을 알 수 있다. 따라서 세 점이 일직선 상에 있는 경우는 결과값에 1이 포함되어 있는지 확인하면 된다.
+) 참고로 A -> B -> C대신 B -> A -> C로 하거나 C -> D -> A대신 D -> C -> A로 해도 결과는 똑같다.
4. 네 점이 일직선 상에 있는 경우

네 점이 일직선 상에 있는 경우 또한 총 3가지 경우가 존재한다. 세 점과는 달리 네 점이 일직선 상에 있는 경우, CCW 결괏값이 전부 0이 되므로 CCW 결과값만으로는 교차 판단을 할 수 없다. 하지만, 겹치지 않는(교차하지 않는) 단 한 가지의 경우를 보면 각 점이 다른 선분 범위에 포함되지 않는다는 것을 알 수 있다. 이 점을 이용해 CCW 결과값이 (0, 0)으로 나왔을 때 추가로 각 점이 다른 선분 범위에 포함되는지 확인하면 선분이 교차하는지 알 수 있다.
+) (0, 0)은 세 점이 일직선 상에 있는 경우 중 2번째 경우에도 나타나는데, 이 경우 또한 각 점이 다른 선분 범위에 포함되므로 교차 판정엔 문제없다.
정리
정리하자면 선분 AB, 선분 CD가 교차하는 조건은 다음과 같다.
- CCW(A, B, C)*CCW(A, B, D) <= 0 && CCW(C, D, A)*CCW(C, D, B) <= 0
- CCW(A, B, C)*CCW(A, B, D) = 0, CCW(C, D, A)*CCW(C, D, B) = 0인 경우, 각 점이 다른 선분 범위에 포함되어야 한다.
구현 코드
#define point pair<long long, long long>
#define line pair<point, point>
using namespace std;
vector<line> lines;
// first => x pos
// second => y pos
int ccw(point A, point B, point C) {
long long res = (B.first - A.first)*(C.second - A.second) - (C.first - A.first)*(B.second - A.second);
return (res > 0) - (res < 0);
}
bool isCross(pair<point, point> l1, pair<point, point> l2) {
point p1 = l1.first;
point p2 = l1.second;
point p3 = l2.first;
point p4 = l2.second;
int p1p2 = ccw(p1, p2, p3) * ccw(p1, p2, p4); // l1 기준
int p3p4 = ccw(p3, p4, p1) * ccw(p3, p4, p2); // l2 기준
// CCW 결과값이 (0, 0)인 경우
if (p1p2 == 0 && p3p4 == 0) {
// 비교를 일반화하기 위한 점 위치 변경
if (p1 > p2) swap(p2, p1);
if (p3 > p4) swap(p3, p4);
return p3 <= p2 && p1 <= p4; // 두 선분이 겹치는 지 확인
}
return p1p2 <= 0 && p3p4 <= 0;
}
참고자료
https://jason9319.tistory.com/358
https://degurii.tistory.com/47
'C++ > 알고리즘' 카테고리의 다른 글
| [알고리즘] 두 포인터(Two-pointer) (0) | 2024.11.04 |
|---|---|
| [알고리즘] 위상 정렬(Topological Sorting) (0) | 2024.11.01 |
| [알고리즘] Union-Find 알고리즘 (0) | 2024.10.29 |
| [알고리즘] 프림 알고리즘(Prim Algorithm), 크루스칼 알고리즘(Kruskal Algorithm) (0) | 2024.10.26 |
| [알고리즘] A* 알고리즘(A star algorithm) (0) | 2024.10.24 |




