나만의 작은 도서관
[알고리즘] Union-Find 알고리즘 본문
Union-Find 알고리즘란?
Union-Find 알고리즘은 서로소 집합(Disjoint Set) 자료구조를 구현하는 알고리즘으로, 서로소 집합들을 효과적으로 관리하기 위해 사용한다. Union-Find 알고리즘은 이름에서도 알 수 있듯 Union과 Find연산을 통해 작동하며, Union은 서로 다른 집합을 하나로 합치는 합연산을, Find는 선택한 원소가 속해있는 집합을 찾는 연산을 한다.
서로소 집합(Disjoint Set)이란?
서로소 집합(Disjoint Set, 분리 집합이라고도 부름)이란 서로 공통된 원소를 가지고 있지 않은 두 개 이상의 집합들을 말한다. 서로소 집합은 특히 동적 연결성을 다루는 문제에 유용하며, 주로 네트워크 연결이나 그래프의 사이클 검출과 같은 문제에 활용할 수 있다.
동작방식
- 초기화(MakeSet)
각 원소에 대한 서로소 집합을 구축한다. 서로소 집합은 해당 원소의 부모 원소를 저장하는 parent 배열로 구축하며, 배열에 저장된 집합 데이터를 트리 자료구조로 표현할 수 있다. 초기에 parent 배열은 부모 원소가 없으므로 자기 자신을 저장하도록 초기화한다.

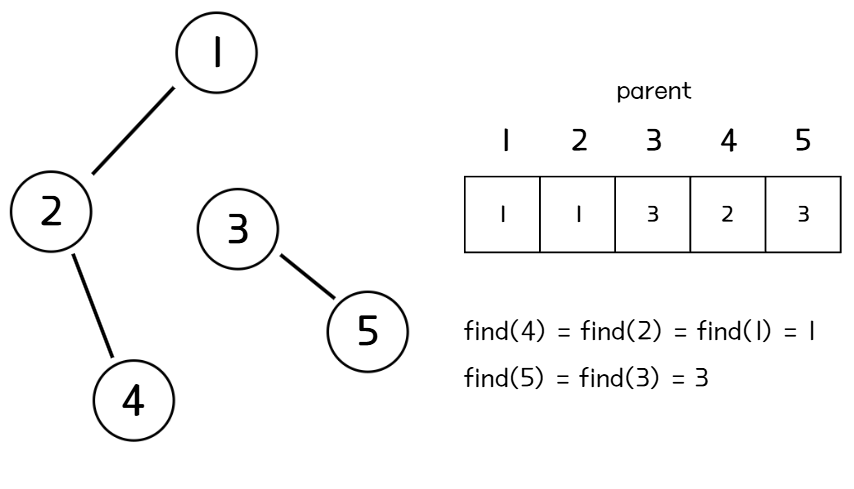
- Find
Find는 선택한 원소가 속해있는 집합을 찾는 연산을 한다. '선택한 원소는 어느 집합에 속해있는가?'를 알기 위해 Find는 속해있는 집합의 대표 원소(루트 노드)를 찾을 때까지 배열을 재귀적으로 순회한다.
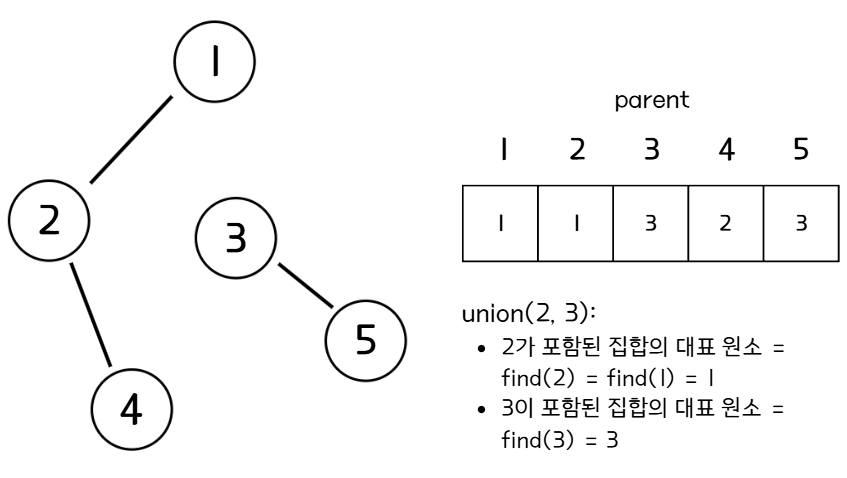
- Union
Union은 두 집합을 하나로 합치는 합연산을 한다. Find연산을 통해 얻은 두 원소의 대표 원소를 비교하고, 두 대표 원소가 다를 경우에만 두 집합을 하나로 합친다. Union연산이 진행되고나면 두 대표 원소 중 하나는 다른 대표 원소를 부모 원소로 갖게 된다.

구현 코드
아래 코드는 위에서 설명한 Union-Find 알고리즘을 가장 naive하게 구현한 코드이다. 이 코드의 문제점은 하나의 트리의 리프 노드에 반복적으로 합쳐 최대 N 깊이를 가진 트리가 만들어질 수 있다는 점이다. 따라서 해당 코드의 시간복잡도는 O(N)이다.
vector<int> parent; // 자기자신으로 초기화가 되어있는 배열
// union-find 알고리즘
int find(int x){
if(parent[x] == x) return x;
return find(parent[x]);
}
bool union_set(int u, int v){
u = find(u);
v = find(v);
// 두 집합이 같은 집합이라면 false반환.
if(u == v) return false;
// 대표 원소의 크기를 기준으로 두 집합을 합친다.
if(u < v) parent[v] = u;
else parent[u] = v;
return true;
}
최적화를 위한 첫번째 방법: 경로 압축(Path Compression)
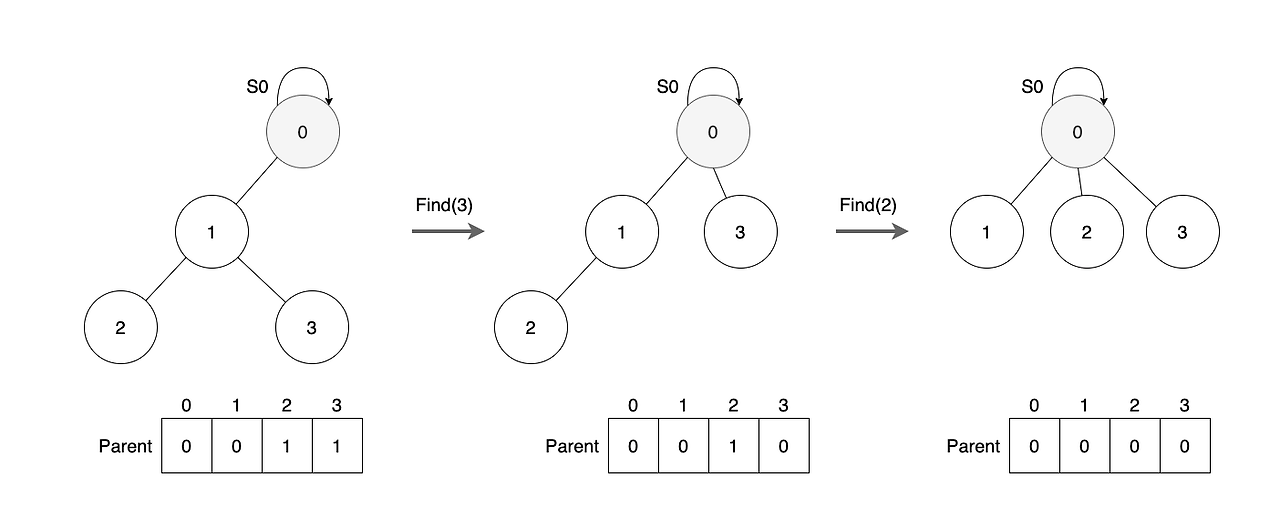
경로 압축은 Find연산을 할 때 탐색하는 모든 원소를 대표 원소로 연결하는 최적화 기법이다. 경로 압축은 탐색한 모든 원소의 부모 원소는 전부 대표 원소로 변경하며, 이를 통해 집합을 표현하는 트리 높이와 Find연산 호출 횟수를 줄일 수 있다.
int find(int x){
if(parent[x] == x) return x;
return parent[x] = find(parent[x]); // 경로 압축
}
최적화를 위한 두번째 방법: Union By Rank

Union 연산을 할 때 두 집합 중 높이가 낮은 트리를 높은 트리에 합쳐 트리의 높이를 줄이는 최적화 방식이다. 비슷한 개념으로 트리의 크기(원소의 개수)가 작은 트리를 큰 트리에 붙이는 Union by Size 방식도 있다. 경로 압축과 Union By Rank를 적용한 코드는 다음과 같다.
vector<int> parent; // 자기자신으로 초기화 되어있는 배열
vector<int> tree_rank; // 트리 랭크(깊이)를 저장하는 배열
// union-find 알고리즘(경로 압축 + union by rank포함)
int find(int x){
if(parent[x] == x) return x;
return parent[x] = find(parent[x]); // 경로 압축
}
bool union_set(int u, int v){
u = find(u);
v = find(v);
// 두 집합이 같은 집합이라면 false반환.
if(u == v) return false;
// 두 집합의 깊이가 같을 경우, 첫번째 집합의 트리 깊이 랭크를 하나 올린다.
// 이는 첫번째 대표 원소를 합친 집합의 대표 원소로 하겠다는 의미이다.
if(tree_rank[u] == tree_rank[v]) tree_rank[u]++;
// 두 집합의 깊이가 다를 경우, 깊이가 깊은 트리에 낮은 트리를 합친다.
if(tree_rank[u] < tree_rank[v]) parent[v] = u;
else parent[u] = v;
return true;
}
모든 원소를 음이 아닌 정수로 표현가능한 경우, "parent 배열을 음수로 초기화 한다면, 대표 원소만 음수값을 가진다"는 아이디어를 활용해 parent 배열에 트리 랭크 정보 또한 저장할 수 있다(음수는 트리의 깊이, 양수는 대표 원소를 의미). 코드는 아래와 같다.
vector<int> parent; // -1로 초기화가 되어있는 배열
// union-find 알고리즘(경로 압축 + union by rank포함)
int find(int x){
if(parent[x] < 0) return x;
return parent[x] = find(parent[x]); // 경로 압축
}
bool union_set(int u, int v){
u = find(u);
v = find(v);
// 두 집합이 같은 집합이라면 false반환.
if(u == v) return false;
// 두 집합의 깊이가 같을 경우, 첫번째 집합의 트리 깊이 랭크를 하나 올린다.
// 이는 첫번째 대표 원소를 합친 집합의 대표 원소로 하겠다는 의미이다.
if(parent[u] == parent[v]) parent[u]--;
// 두 집합의 깊이가 다를 경우, 깊이가 깊은 트리에 낮은 트리를 합친다.
if(parent[u] < parent[v]) parent[v] = u;
else parent[u] = v;
return true;
}
짚고 넘어가야 할 점
최종 시간복잡도?
경로 압축과 Union By Rank를 사용한 Union-Find 알고리즘의 각 연산은 거의 상수 시간에 수행된다. 엄밀히 말하자면 상수 시간이 아닌, α(N)에 비례하는 시간 복잡도를 가지는데, 여기서 α(N)는 아커만 함수의 역함수를 말한다. 아커만 함수의 역함수는 매우 천천히 증가하는 함수이므로, 사실상 거의 상수 시간이라고 봐도 무방하다.
참고자료
'C++ > 알고리즘' 카테고리의 다른 글
| [알고리즘] 위상 정렬(Topological Sorting) (0) | 2024.11.01 |
|---|---|
| [알고리즘] CCW(Counter ClockWise)와 선분 교차 판정 (1) | 2024.10.30 |
| [알고리즘] 프림 알고리즘(Prim Algorithm), 크루스칼 알고리즘(Kruskal Algorithm) (0) | 2024.10.26 |
| [알고리즘] A* 알고리즘(A star algorithm) (0) | 2024.10.24 |
| [알고리즘] 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2024.10.23 |




