나만의 작은 도서관
[알고리즘] 너비 우선 탐색(BFS)와 dx, dy 테크닉 본문
너비 우선 탐색(BFS)이란?
너비 우선 탐색(BFS, Breadth First Search)은 그래프 탐색을 진행할 때 깊이와 너비 중 너비를 우선적으로 탐색하는 방식을 의미하며, 깊이 우선 탐색(DFS, Depth First Search)와 동일하게 완전 탐색 알고리즘으로 분류된다.
BFS를 이용한 그래프 탐색의 시간복잡도: O(V+E) or O(V^2)
너비 우선 탐색은 깊이 우선 탐색과 동일하게 그래프에 존재하는 모든 정점들을 탐색하는 것이 주 목적이다. 따라서 너비 우선 탐색 또한 그래프가 어떻게 표현되었는가에 따라 시간복잡도가 다음과 같아진다.
그래프의 정점(Vertex)수를 V, 간선(Edge)수를 E라고 했을 때,
- 그래프가 인접 리스트로 표현된 경우 O(V + E)
- 그래프가 인접 행렬로 표현된 경우 O(V^2)
너비 우선 탐색 동작방식
1. 시작점 선택
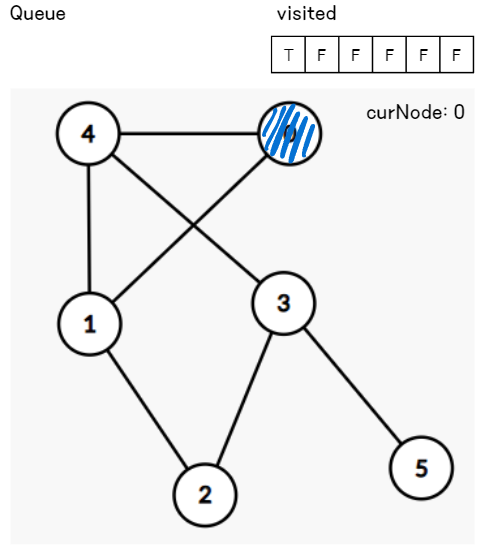
탐색을 시작할 노드(다른 말로 정점)를 선택한다. 선택한 노드는 루트 노드(level 0)가 된다. 아래 예시에서는 시작점으로 0번 노드를 선택했다.

2. 방문 기록
시작점을 선택했다면 해당 노드를 방문한 사실을 기록한다. 방문 여부는 별도의 리스트(배열, 집합 등)를 통해 기록한다. 또한 자료구조 큐(Queue)에 해당 노드를 삽입한다.

2. 큐에서 노드 추출
큐에서 노드를 하나 꺼낸다. 꺼낸 노드는 현재 탐색 중인 노드가 된다.
3. 인접 노드 탐색
현재 노드에 인접한 모든 노드 중에서 아직 방문하지 않은 노드들을 큐에 추가한다.

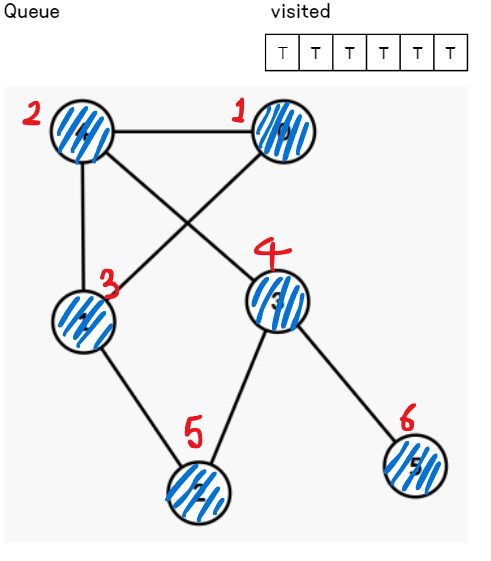
4. 큐가 빌 때까지 반복
더이상 방문 가능한 노드가 없어 큐가 빌 때까지 2~3 과정을 반복한다.



5. 종료
큐가 비었다면 탐색을 종료한다.
dx, dy 테크닉
dx, dy 테크닉은 격자 속 상하좌우로 움직이는 코드를 깔끔하게 구현하는 테크닉이다. 아래 그림과 같이 동서남북 4방향에 대한 x축, y축 방향값을 각각 dx, dy배열에 저장하여 구현한다. 아래 그림에서 dx, dy에 저장된 값의 의미는 차례대로 동 -> 남 -> 서 -> 북(시계방향)이지만, 탐색 순서에 대한 조건이 따로 없다면 방향에 대한 순서는 상관없다.

dx, dy 테크닉을 코드로 구현하면 아래와 같다.
int dx[DIR] = { 0, 1, 0, -1 };
int dy[DIR] = { 1, 0, -1, 0 };
int r = 10, c = 11;
for (int i = 0; i < DIR; i++) {
int nx = r + dx[i];
int ny = c + dy[i];
cout << nx << " " << ny << '\n';
}
// 출력 결과
10 12
11 11
10 10
9 11
구현 코드(BFS + dx, dy테크닉)
int N, M;
vector<vector<int>> matrix;
vector<vector<bool>> visited;
// 해당 (x, y)좌표가 격자를 벗어나는 지 확인
bool inRange(int r, int c) {
return 0 <= r && r < N && 0 <= c && c < M;
}
void bfs(int r, int c) {
int dx[DIR] = { 0, 1, 0, -1 };
int dy[DIR] = { 1, 0, -1, 0 };
queue<pair<int, int>> q;
q.push(make_pair(r, c));
visited[r][c] = true;
// 큐(Queue)가 빌 때까지 반복
while (!q.empty()) {
pair<int, int> p = q.front();
q.pop();
// 동서남북 4방향을 순차대로 방문
for (int i = 0; i < DIR; i++) {
int nx = p.first + dx[i];
int ny = p.second + dy[i];
if (inRange(nx, ny) && matrix[nx][ny] && !visited[nx][ny]) {
q.push(make_pair(nx, ny));
visited[nx][ny] = true;
matrix[nx][ny] = matrix[p.first][p.second] + 1;
}
}
}
}
짚고 넘어가야 할 점
BFS는 어떤 상황에서 왜 써야할까?
사실 BFS를 사용했다고 DFS보다 눈에 띄게 빠르지는 않지만, 탐색할 노드들을 큐에 저장하고 있기 때문에 훨씬 메모리를 많이 차지한다. 그럼에도 불구하고 BFS를 사용하는 이유가 있는데 그 이유들은 다음과 같다.
- 최단 거리를 찾는데 유용함
DFS도 최단거리를 찾을 수 있지만 BFS를 통해 최단 거리를 찾으면 처음 방문한 노드는 항상 최단거리라는 것을 보장하며, 얕은 level부터 차례대로 탐색한다는 장점이 있다. 이러한 장점을 살려 모든 노드에 대한 최단거리를 한 번에 찾을 수 있고, 노드의 탐색할 때 level별로 분리하여 탐색할 수도 있으며, 도착지가 출발지와 가까운 경우 DFS보다 훨씬 빠르게 최단 거리를 찾는다. 게다가 무한한 그래프와 같은 특정한 상황에서 DFS가 찾지 못하는 경로를 BFS가 찾아내기도 한다. - 사용의 편리함
이건 개인적인 취향이지만, 그래프 탐색을 할 때 BFS를 사용할 수 있는 문제라면 무조건 BFS로 탐색한다. 왜냐하면 재귀함수를 사용하는 것 자체가 오류를 만들어내는 경우가 많고, 이것저것 추가 조건을 요구하는 문제에서 BFS를 사용했을 때조건을 추가하기 훨씬 쉽기 때문이다. 아래에서 설명할 분기한정법이나 최고 우선 탐색과 같은 최적해를 찾기 위한 최적화 방법도 있어 확장성도 높아 다양한 문제에 적용할 수 있다.
최적화 문제에서 BFS를 최적화하는 방법: 분기한정 알고리즘(branch and bound)
분기한정 알고리즘은 상태공간트리를 사용하여 문제를 푼다는 점에서 백트래킹과 매우 비슷하지만, 1) 트리 횡단방법에 구애받지 않고, 2) 최적화 문제를 푸는데만 사용된다는 점이 다르다. 분기한정 알고리즘은 어떤 노드가 유망한지를 결정하기 위해 그 노드에 한계값(bound)를 설정한다. 그리고나서 현재의 최적값과 비교하여 최적값보다 낮다면 유망하지 않은 노드라 판단한다. 분기한정을 백트래킹에 추가할 수도 있지만, 분기한정의 장점을 잘 살리지 못하기 때문에 BFS 탐색 방식에 추가하는 것이 일반적이다. 이렇게 분기한정을 추가하게되면 보다 넓은 범위에서 유망하지 않은 노드를 알아낼 수 있다.
한 번 더 최적화하는 방법: 최고 우선 탐색(Best First Search)
BFS는 큐에 저장되어 있는 탐색할 노드들이 저장된 순서는 탐색한 순서대로 저장할 뿐, '최적값이 될 수 있는 가능성이 높은가?'와는 전혀 관련이 없다. 따라서 큐에 저장되어 있는 탐색할 노드들을 최적값이 될 가능성이 높은 순으로 정렬하여, 보다 빠르게 최적값을 구할 수 있도록 개선한 방식을 최고 우선 탐색(Best First Search)라고 한다.
분기한정 알고리즘과 상관없이 독립적으로 최고 우선 탐색을 사용할 수 있지만, 현재의 최적값이 최종 최적값과 가까울수록 더 많은 노드들을 유망하지 않다고 판단할 수 있기 때문에 같이 사용할 경우 시너지 효과를 기대할 수 있다.
이러한 최고 우선 탐색을 코드로 구현하는 것은 비교적 간단하다. 최적값에 대한 정렬 기준을 세운 다음, 기존의 큐를 그 정렬 기준을 적용한 우선순위 큐로 변경하기만 하면 된다.
+) 분기한정 알고리즘과 최고 우선 탐색에 대한 자세한 내용은 나중에 시간이 되면 다룰 예정이다.
참고자료
알고리즘 기초 - Richard E. Neapolitan
알고리즘 트레이닝 북 (PROGRAMMING CHALLENGES) - 스티븐 스키에나 외 저자
'C++ > 알고리즘' 카테고리의 다른 글
| [알고리즘] 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm) (0) | 2024.10.16 |
|---|---|
| [알고리즘 부록] 트리를 순회하는 방법 3가지(프리오더, 인오더, 포스트오더) (1) | 2024.10.16 |
| [알고리즘] 백트래킹(backtracking)과 깊이 우선 탐색(DFS) (0) | 2024.10.13 |
| [알고리즘] 최대공약수(GCD)와 유클리드 호제법(Euclidean algorithm) (0) | 2024.10.12 |
| [알고리즘] 소수 판별법과 에라토스테네스의 체 (2) | 2024.10.11 |





