나만의 작은 도서관
[알고리즘] 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm) 본문
플로이드-워셜 알고리즘(Floyd-Warshall Algorithm)이란?
플로이드-워셜 알고리즘은 가중치가 있는 그래프(weighted graph)에서 모든 정점 쌍 사이의 최단 경로 길이를 구하는 알고리즘이다. 플로이드-워셜 알고리즘은 이전 단계에서의 최단 경로 길이를 저장해두었다가 현재 단계에서의 최단 경로 길이를 구할 때 재사용하기 때문에 다이나믹 프로그래밍(dynamic programming) 알고리즘으로 분류된다.
점화식
플로이드-워셜 알고리즘은 다이나믹 프로그래밍 알고리즘으로 분류되기때문에 점화식이 존재한다. 정점 i를 vi, k번 이하의 정점들만 거쳐서 vi에서 vj로 가는 최단 경로 길이를 dist(k, i, j)라 했을 때(1 <= k <= N), 점화식은 다음과 같다.
dist(k, i, j) = min( dist(k-1, i, j), dist(k-1, i, k) + dist(k-1, k, j) )
간단하게 설명하자면 vk를 거치는 최단 경로 길이와 그렇지 않은 최단 경로 길이 중 작은 값이 k번 이하의 정점들만 거쳤을 때 vi에서 vj로 가는 최단 경로 길이라는 뜻이다.
점화식 증명
아래 그림처럼 k-1번 이하의 정점들을 거쳤을 때 vi에서 vj로 가는 최단 경로가 있다. 중간으로 거쳐갈 수 있는 모든 정점들을 지나가본 결과이니 최단 경로에 대한 의심의 여지가 없다. (그림은 vi에서 vj로 바로가는 것처럼 표현했지만, 중간에 거쳐가는 정점들을 생략한 것이다.)

하지만 여기서 k번 이하의 정점들을 거쳤을 때 vi에서 vj로 가는 최단 경로를 구하는 경우로 변경한다면 어떨까? 정점 k를 거쳐가는 경로가 추가로 생김으로써 이전의 최단 경로가 현재의 최단 경로라 보장할 수 없다.

따라서, 현재의 최단 경로(k번 이하의 정점들을 거쳤을 때 vi에서 vj로 가는 최단 경로)는 정점 k를 거쳐가는 최단 경로와 이전 최단 경로의 길이 중 작은 값이 된다. 여기서 k번 정점을 거쳐가는 최단 경로 길이는 vi~vk의 최단 경로 길이와 vk~vj의 최단 경로길이의 합으로, 이 둘 모두 이전 단계에서 구할 수 있기 때문에 따로 구할 필요없이 재사용하면 된다.(참고로, 이전 단계의 최단 경로들은 k-1번 이하의 정점만 거쳐가므로, k번 정점을 거쳐가는 경우는 존재하지 않는다)


시간복잡도 O(N^3)
플로이드-워셜 알고리즘은 N번에 거쳐 모든 정점 간의 최단 경로의 길이를 N*N 번 반복하여 구하기 때문에 O(N^3)이라는 무지막지한 시간복잡도를 가지고 있다. 하지만 한 번에 모든 정점 간의 최단 경로 길이를 구할 수 있다는 점 때문에 많은 양의 최단 경로 길이를 요구하는 문제에서는 유용하게 쓸 수 있다.
동작방식

1. 초기화
- 주어진 그래프를 vi -> vj 경로의 길이(또는 가중치)를 저장하는 2차원 배열로 표현한다(graph). 자기 자신으로 가는 경로는 0, 직접 연결되어 있지 않은 경로는 무한대(INF)로 설정한다.
- 각 단계의 최단 경로 길이를 저장할 3차원 배열(dist)의 0번째를 그래프와 동일하게 설정한다.
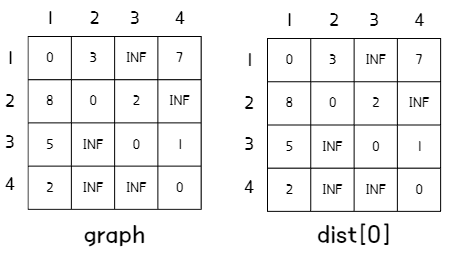
2. 점화식 사용
- 위에서 설명한 점화식 dist(k, i, j) = min( dist(k-1, i, j), dist(k-1, i, k) + dist(k-1, k, j) )를 (1, 1) ~ (N, N)까지 적용하여 k번째 단계의 2차원 배열에 들어갈 값을 구한다.
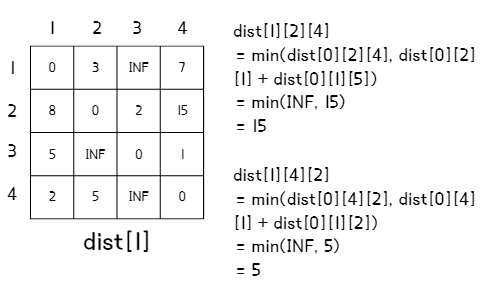
3. 2번 과정을 N번 반복
- N번째 단계까지 2번 과정을 반복한다.
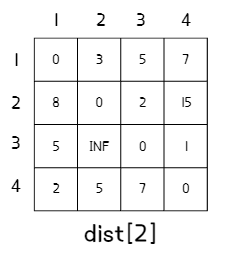
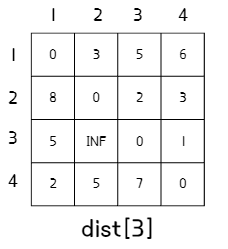
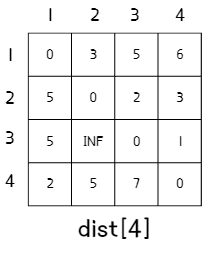
4. 최종 결과
- 반복이 끝나고 만들어진 N번째 단계의 2차원 배열이 최단 경로 길이를 저장하고 있는 2차원 배열이 된다.

구현 코드
void floyd(int N, vector<vector<int>>& graph, vector<vector<vector<int>>>& dist){
dist[0] = graph; // dist 초기화
for(int k = 1; k <= N; k++){
for(int i = 1; i <= N; i++){
for(int j = 1; j <= N; j++){
if(i == j) continue;
dist[k][i][j] = min(dist[k-1][i][j], dist[k-1][i][k] + dist[k-1][k][j]);
}
}
}
}
최적화가 가능할까?
위 코드는 메모리적인 관점에서 최적화가 가능하다. 최단 경로 길이를 저장하는 3차원 배열(dist)을 2차원 배열로 차원을 줄일 수가 있는데, 이렇게 각 단계에 대한 배열을 따로 갖지 않고 2차원 배열 하나만으로 계산할 수 있는 이유는 아래와 같다.
1. k단계의 k행, k열에 있는 값들은 k-1단계와 동일하다.
점화식에서 i = k, j = k를 대입한 경우를 구해보면 금방 알 수 있는데, 이를 대입해보면 다음과 같다.
점화식: dist(k, i, j) = min( dist(k-1, i, j), dist(k-1, i, k) + dist(k-1, k, j) )
if) i = k인 경우
dist(k, k, j) = min( dist(k-1, k , j), dist(k-1, k, k) + dist(k-1, k, j) )
dist(k-1, k, k) = 0이므로, min( dist(k-1, k, j), dist(k-1, k, k) + dist(k-1, k, j) ) = dist(k, k, j)
∴ dist(k-1, k, j) = dist(k, k, j)
if) j = k인 경우
dist(k, i, k) = min( dist(k-1, i, k ), dist(k-1, i, k) + dist(k-1, k, k) ) = dist(k-1, i, k)
dist(k-1, k, k) = 0이므로, min( dist(k-1, i, k ), dist(k-1, i, k) + dist(k-1, k, k) ) = dist(k, i, k)
∴ dist(k-1, i, k) = dist(k, i, k)
따라서, 위 풀이를 통해 i = k, j = k인 경우 k단계의 k행, k열에 있는 값들은 k-1단계와 동일하다는 것이 증명되었다.
2. 오로지 자기자신만이 이전 단계의 자기자신의 값을 참조한다. (단, k행, k열 제외)
같은 메모리에서 갱신과 참조 둘 다 진행하는 경우, 갱신된 값을 참조하여 잘못된 값을 가져오는 것이 문제가 된다. 하지만, 플로이드-워셜 알고리즘에서는 현재 단계에서 오로지 자기자신만이 이전 단계의 자기자신 값을 참조하기 때문에 같은 메모리에서 갱신과 참조 둘 다 진행하여도 현재 단계에서 갱신된 값을 참조하는 경우는 발생하지 않는다.
위 2가지 이유를 근거로 각 단계를 저장하지 않고 하나의 2차원 배열만을 사용함으로써 메모리를 절약하고도 같은 결과를 기대할 수 있다. 코드로 구현하면 아래와 같다.
최적화한 코드
void floyd2(int N, vector<vector<int>>& graph, vector<vector<int>>& dist){
dist = graph; // dist 초기화
for(int k = 1; k <= N; k++){
for(int i = 1; i <= N; i++){
for(int j = 1; j <= N; j++){
if(i == j) continue;
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}
최단 경로 추적하기
만약 최단 경로 길이와 더불어 최단 경로를 추적하고 싶다면, 2차원 배열을 하나 만들어 최단 경로가 정점 k를 지나가는 경로로 갱신될 때마다 (i, j)위치에 k를 저장하는 코드를 추가하여 구현할 수 있다. 이는 vi -> vj에 대한 최단 경로 사이에 정점 k가 존재함을 의미함으로써 k를 중심으로 중위 순회(inorder)하면 최단 경로를 출력할 수 있다.
최단 경로 추적 코드를 추가
void floyd2(int N, vector<vector<int>>& graph, vector<vector<int>>& dist, vector<vector<int>>& path){
dist = graph; // dist 초기화
for(int k = 1; k <= N; k++){
for(int i = 1; i <= N; i++){
for(int j = 1; j <= N; j++){
if(i == j) continue;
if(dist[i][k] + dist[k][j] < dist[i][j]){
path[i][j] = k;
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
}
// 중위 순회(inorder)방법으로 경로를 출력.
void printPath(vector<vector<int>>& path, int s, int t){
// 0은 s과 t 사이에 중간 마디가 없음을 의미
if(path[s][t] != 0){
printPath(path, s, path[s][t]);
cout << path[s][t] << " ";
printPath(path, path[s][t], t);
}
}짚고 넘어가야 할 점
음의 가중치가 있는 경우
플로이드-워셜 알고리즘은 음의 가중치가 존재하는 경우에도 최단 경로를 구할 수 있다. 하지만 그래프 내에 음의 사이클(사이클에 포함된 경로의 합이 음수인 경우)이 존재하면 무한히 사이클을 돌며 결국엔 최단 경로의 길이가 음의 무한대가 나오기 때문에 음의 사이클이 존재하는 지 판별해야한다.
다행히 플로이드-워셜 알고리즘에서도 음의 사이클을 판단할 수 있는데, i = j인 경우 dist[i][j]값이 0이 아닌 음수 값이 나왔을 때 음의 사이클이 존재한다고 판단한다. ( 해당 정점에서 제자리로 돌아오는 경로가 음수인 경우는 해당 정점을 포함하는 음의 사이클이 존재하는 경우 밖에 없다.)
참고자료
'C++ > 알고리즘' 카테고리의 다른 글
| [알고리즘] 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2024.10.23 |
|---|---|
| [알고리즘] 다익스트라 알고리즘(Dijkstra Algorithm) (1) | 2024.10.19 |
| [알고리즘 부록] 트리를 순회하는 방법 3가지(프리오더, 인오더, 포스트오더) (1) | 2024.10.16 |
| [알고리즘] 너비 우선 탐색(BFS)와 dx, dy 테크닉 (0) | 2024.10.14 |
| [알고리즘] 백트래킹(backtracking)과 깊이 우선 탐색(DFS) (0) | 2024.10.13 |





