나만의 작은 도서관
[Data Structure] 최대 / 최소 힙 본문
최대 / 최소 힙이란?
최대 / 최소 힙은 이진 트리(Binary Tree, BST)의 한 종류로, 우선순위가 높은 값에 빠르게 접근하기 위해 고안된 방법이다. 각 노드는 2가지 규칙을 따라야 하며, 규칙은 아래와 같다.
조건 #1. 완전 이진 트리여야 한다.
조건 #2. 모든 노드의 키 값은 자식 노드의 키 값보다 우선순위가 높거나 같아야한다.
조건 2에서 큰 값이 우선 순위가 높다면 최대 힙, 작은 값이 우선 순위가 높다면 최소 힙이 된다.
최대 / 최소 힙의 특징
- 완전 이진 트리이다.
- 왼쪽 서브 트리와 오른쪽 서브트리는 서로 관련이 없다. 오로지 부모 노드랑만 관련있다.
- 중복값을 허용한다.
완전 이진 트리(Complet Binary Tree)란?
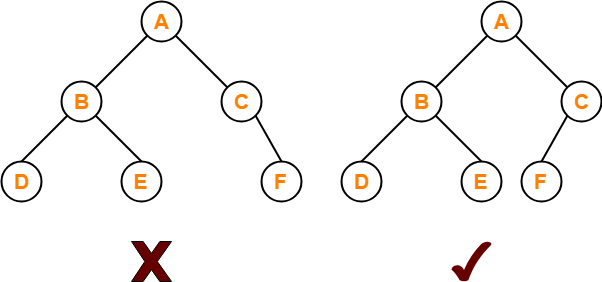
이진 트리에 노드를 삽입할 때 왼쪽부터 차례대로 삽입하는 트리이다. 위 그림의 왼쪽 트리처럼 왼쪽부터 차례대로 삽입되지 않은 트리는 완전 이진 트리라고 할 수 없다.
삽입 과정

- 마지막 노드(최하단부 가장 오른쪽 노드) 다음 위치에 삽입한다.
- 만약 부모 노드의 값보다 우선 순위가 높다면 위치를 swap한다.
- 조건 #2 ("모든 노드의 키 값은 자식 노드의 키 값보다 우선순위가 높거나 같아야한다.")를 만족할때까지 2번 과정을 반복한다. (루트 노드 방향으로 점점 올라간다.)
삭제 과정

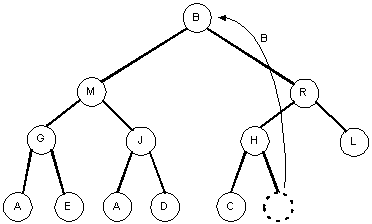

- 루트 노드를 삭제한다.
- 마지막 노드(최하단부 가장 오른쪽 노드)를 루트 노드로 이동시킨다.
- 만약 이동한 노드의 값이 자식 노드의 값보다 우선 순위가 낮다면 위치를 swap한다.
- swap시, 두 자식 노드 중 우선순위가 높은 자식 노드와 swap한다. (그렇지 않으면 조건 #2에 위배된다)
- 조건 #2 ("모든 노드의 키 값은 자식 노드의 키 값보다 우선순위가 높거나 같아야한다.")를 만족할때까지 3번 과정을 반복한다. (리프 노드 방향으로 점점 내려간다.)
최종 결과

시간복잡도
최대 / 최소 힙에서 노드의 삽입 / 삭제 자체의 시간복잡도는 O(1)이다. 하지만 노드를 삽입 / 삭제 작업을 완료하려면 조건 #2를 만족할때까지 swap을 반복해야하기때문에 실제 삽입 / 삭제 작업을 완료하는 데 걸리는 시간은 swap 작업의 시간복잡도를 따라간다. (swap 작업이 삽입 / 삭제보다 느리기 때문) 따라서, 최종 시간복잡도는 아래와 같다.
| swap | 삽입 | 삭제 | |
| 시간 복잡도 | O(logN) | O(logN) | O(logN) |
C++에서의 힙 사용
C++에서 priority_queue가 힙 자료구조를 사용한다. 기본 설정으로 최대 힙이 설정되어 있다.
priority_queue<int> pq; // 힙 자료구조 사용. (기본값은 최대 힙)
참고 자료
https://azrael.digipen.edu/~mmead/www/Courses/CS280/Heaps-1.html
'Common > CS-일반' 카테고리의 다른 글
| [Data Structure] 이진 검색 트리(Binary Search Tree) (0) | 2025.03.11 |
|---|---|
| [OS] 내부 단편화, 외부 단편화 (0) | 2025.03.10 |
| [OS] 페이지(Page) (0) | 2025.03.10 |
| [OS] 가상 주소(Virtual Address) (0) | 2025.03.10 |
| [OS] 프로세스의 메모리 구조 (0) | 2025.02.19 |




