나만의 작은 도서관
[Data Structure] 이진 검색 트리(Binary Search Tree) 본문
이진 검색 트리(Binary Search Tree)란?

이진 검색 트리는 이진 트리(Binary Tree, BST)의 한 종류로, 각 노드가 1가지 규칙을 따르는 자료구조이다. 규칙은 다음과 같다.
왼쪽 서브트리에 있는 모든 값은 부모 노드의 값보다 작으며, 오른쪽 서브트리에 있는 모든 값은 부모 노드의 값보다 크다.
이진 검색 트리의 특징
- 중위 순회 시 오름차순으로 정렬된 결과를 얻을 수 있다.
- 트리의 최솟값은 가장 왼쪽 노드에, 최댓값은 가장 오른쪽 노드에 배치된다.
선임자(Predecessor)와 후임자(Succesor)
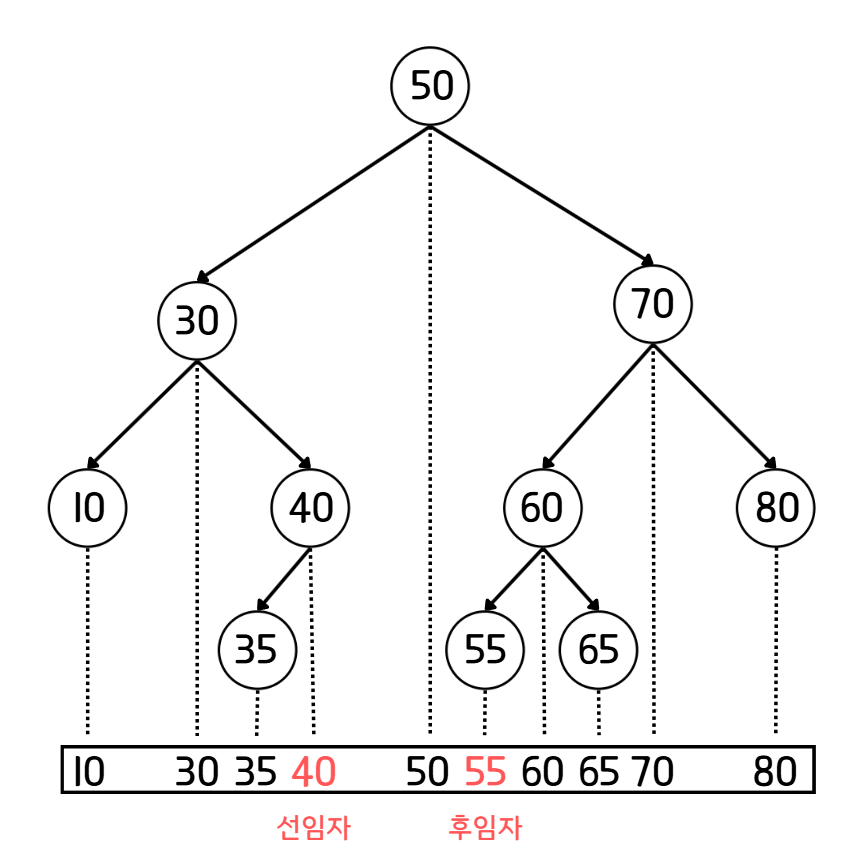
이진 검색 트리에는 선임자와 후임자라는 개념이 존재한다. 선임자와 후임자는 삭제 작업 시 사용되며, 의미는 아래와 같다.
- 선임자(Predecessor) : 노드에 저장된 값보다 작은 값 중 가장 큰 값을 가진 노드.
- 왼쪽 서브트리에서 가장 오른쪽에 있는 노드가 선임자가 된다.
- 후임자(Succesor): 노드에 저장된 값보다 큰 값중 가장 작은 값을 가진 노드.
- 오른쪽 서브트리에서 가장 왼쪽에 있는 노드가 후임자가 된다.
중복된 값에 대한 처리
일반적인 경우 이진 검색 트리는 "중복된 값은 없는" 상황에서 사용한다. 하지만 그렇다고 중복된 값이 존재할 때 사용할 수 없는 건 아니다. 중복된 값이 존재할 때 이진 검색 트리는 크게 아래 2가지 방법으로 처리한다.
1. 중복된 값을 자식 노드에 배치
10
/ \
5 15
/ \
15 20- 중복 노드를 왼쪽 또는 오른쪽 자식 노드에 배치하는 방법이다. 중복 노드 삽입 시 왼쪽, 오른쪽 중 하나로 통일해야 하는데, 일반적으로 오른쪽 자식 노드에 삽입한다.
- 이 방식은 구현이 간단하다는 장점이 있지만, 특정 값이 편향될 가능성이 있다는 단점이 있다.
2. 각 노드에 중복 카운트 추가
(10, 2)
/ \
(5, 1) (15, 3)- 각 노드에 값과 함께 카운트도 저장하는 방법이다. 중복된 값을 가진 노드를 삽입하면, 기존 노드의 카운트를 1 증가시킨다.
- 이 방식은 1번 방식보다 트리의 균형을 잘 유지하면서, 중복 데이터를 효율적으로 저장할 수 있다는 장점이 있다. (대신, 코드가 약간 복잡해지기는 한다.)
검색 과정
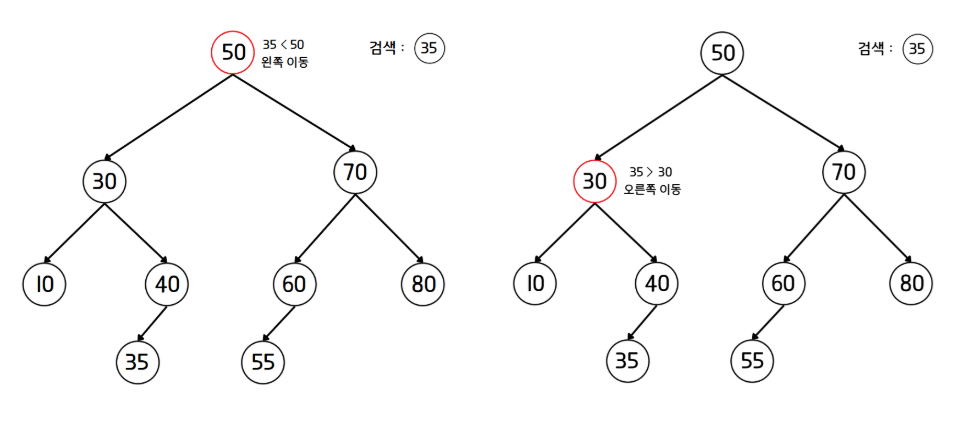
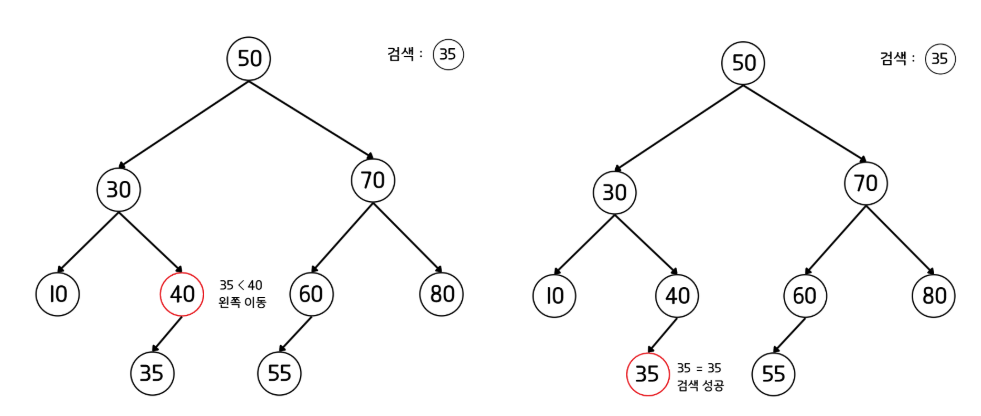
- 루트 노드에 있는 값과 검색 값을 비교한다.
- 값이 검색 값과 일치하다면 검색을 종료한다. 일치하지 않을 경우, 검색 값이 더 작으면 왼쪽 자식 노드로, 더 크다면 오른쪽 자식 노드로 이동한다.
- 더 이상 이동하지 못할 때까지 2번 과정을 반복한다.
- 더 이상 이동할 수 있는 노드가 없다면 검색은 실패한 상태로 종료한다.
삽입 과정

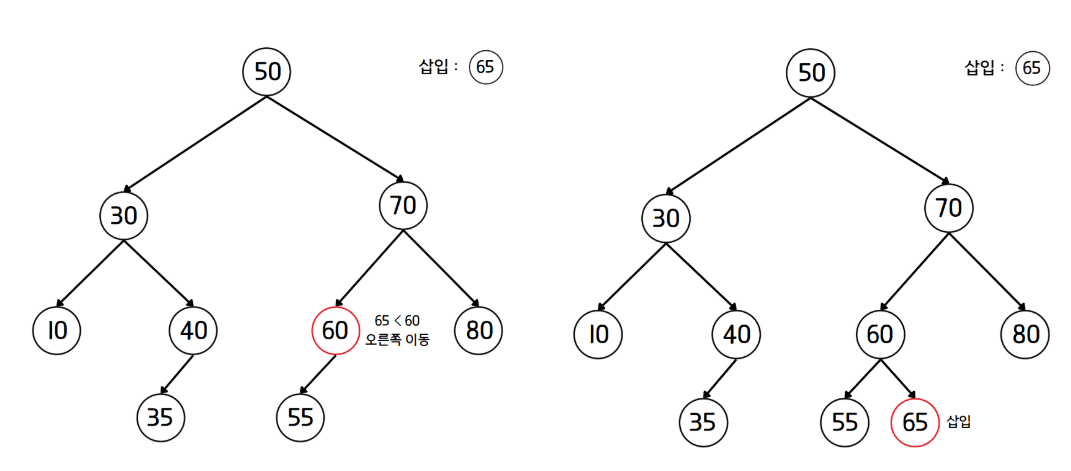
- 검색과 같은 방식으로 삽입 노드의 값이 더 작으면 왼쪽 자식 노드로, 더 크다면 오른쪽 자식 노드로 이동한다.
- 더 이상 이동하지 못할 때까지 1번 과정을 반복한다.
- 더 이상 이동할 수 있는 노드가 없다면 해당 위치에 노드를 삽입한다.
삭제 과정

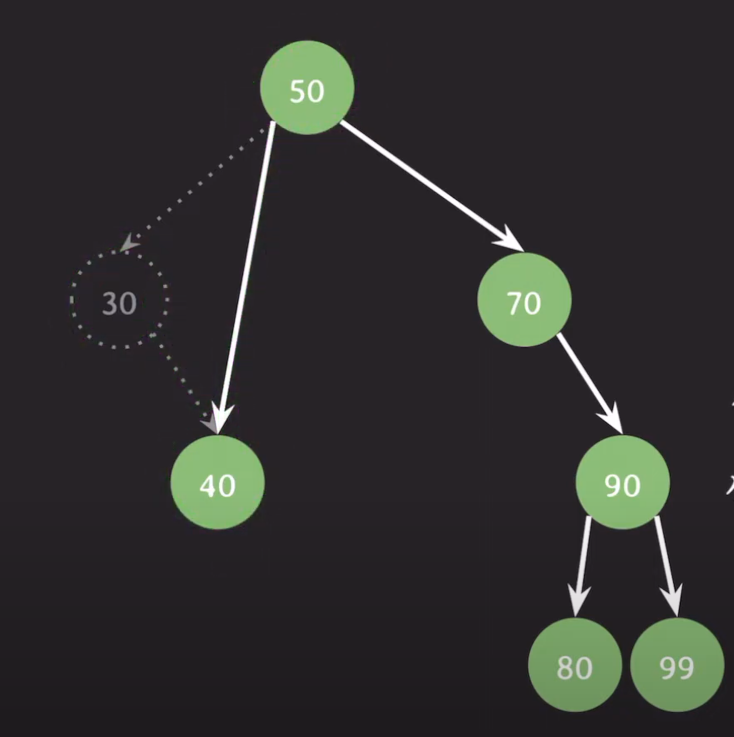
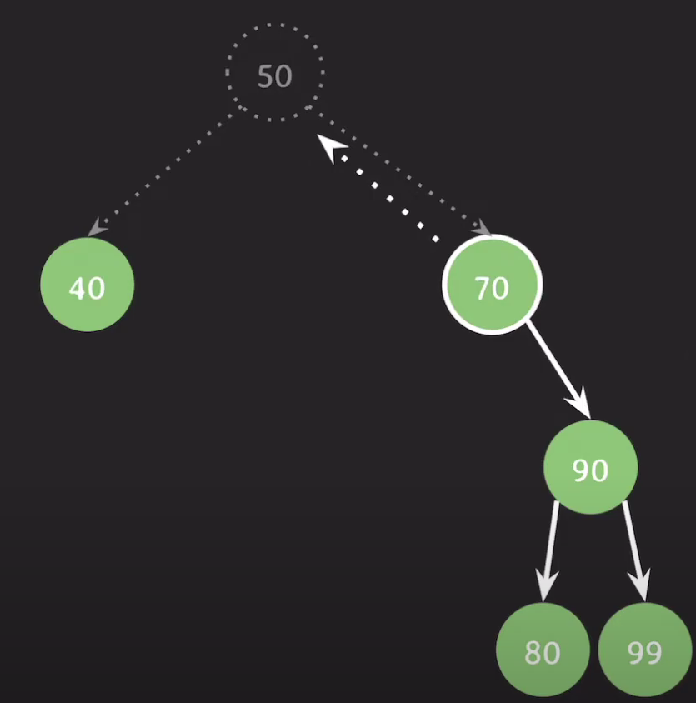
- 삭제할 노드의 위치를 검색 과정을 통해 이동한 후, 해당 노드를 삭제한다. (검색에 실패한 경우, 삭제는 실패한 상태로 종료한다.)
- 노드를 삭제한 후, 아래 세 가지 경우로 나눠 처리한다.
- 자식이 없는 경우: 아무것도 하지 않는다.
- 자식이 하나인 경우: 삭제된 노드의 부모 노드와 자식노드를 연결한다.
- 자식이 두 개인 경우: 삭제된 노드의 자리를 선임자 또는 후임자 노드가 계승받는다. 일반적으로 후임자 노드를 계승한다.
시간복잡도
이진 검색 트리에서 노드의 삽입 / 삭제 자체의 시간복잡도는 O(1)이다. 하지만 노드를 삽입 / 삭제하려면 해당 위치로 이동해야하기 때문에 실제 삽입 / 삭제 작업을 완료하는 데 걸리는 시간은 검색 작업의 시간복잡도를 따라간다. (검색 작업이 삽입 / 삭제보다 느리기 때문) 따라서, 최종 시간복잡도는 아래와 같다.
이진 검색 트리 시간복잡도
| 검색 | 삽입 | 삭제 | |
| 최적의 경우 시간복잡도 | O(1) | O(1) | O(1) |
| 평균적인 시간복잡도 | O(logN) | O(logN) | O(logN) |
| 최악의 경우 시간복잡도 | O(N) | O(N) | O(N) |
이진 검색 트리의 문제점과 해결책

문제점
위 시간복잡도 표를 보게 되면 최악의 경우 시간복잡도가 O(N)인 것을 알 수 있다. 이는 이진 검색 트리가 값의 삽입 순서에 따라 편향된 트리(skewed tree)가 만들어지는, 즉, 균형이 깨지는(unbalancing) 상황이 발생하기 때문이다. 예를 들어, 값의 삽입 순서가 10 -> 20 -> 30 -> ... 과 같이 정렬된 순서라면, 노드가 오른쪽 자식 노드로만 삽입되면서 편향된 트리가 만들어진다. 이 경우 linked-list와 다를 바 없어 검색 작업의 시간 복잡도가 O(N)이 된다.
해결책
이진 검색 트리에서 최악의 시간복잡도가 O(N)이 나오는 원인은 트리의 균형이 깨졌기 때문이다. 따라서 시간복잡도를 개선하기 위해선 트리의 균형이 깨지지 않도록 유지해야 하는데, 균형을 삽입 / 삭제할 때마다 잡아줘 성능을 개선한 이진 트리를 "자가 균형 이진 트리"라고 한다. 오늘날 사용하는 자가 균형 이진 트리는 대표적으로 아래 2가지가 있다.
자가 균형 이진 트리
- AVL 트리: 삽입 / 삭제 시 루트 노드까지 거슬러 올라가며 균형이 맞는지 balance factor를 이용해 체크하며, 균형이 깨졌을 경우 균형을 맞춰주는 방식의 트리.
- 레드-블랙 트리(RB-Tree) : 삽입 / 삭제 시 레드-블랙 트리의 5가지 속성(property)을 만족하는지 체크하며, 만족하지 못하는 경우 트리를 재구성(reconstructing)하거나 노드의 색깔을 변경(recoloring)한다. 5가지 속성을 만족할 경우, 트리의 균형을 유지된다.
참고 자료
https://yoongrammer.tistory.com/71
https://www.youtube.com/watch?v=i57ZGhOVPcI
'Common > CS-일반' 카테고리의 다른 글
| [Data Structure] 최대 / 최소 힙 (0) | 2025.03.12 |
|---|---|
| [OS] 내부 단편화, 외부 단편화 (0) | 2025.03.10 |
| [OS] 페이지(Page) (0) | 2025.03.10 |
| [OS] 가상 주소(Virtual Address) (0) | 2025.03.10 |
| [OS] 프로세스의 메모리 구조 (0) | 2025.02.19 |




