나만의 작은 도서관
[TIL] 240511 캠프 27일차: 분할정복을 이용한 거듭제곱 본문
오늘의 한 마디: 주말에도 TIL을 써볼까하는데 이게 약이 될 지, 독이 될 지 잘 모르겠다. 일단은 한 번 써보기로?
오늘 배운 내용
모듈로(나머지) 연산의 성질
모듈로 연산에는 다음과 같은 성질들이 있다. 해당 성질들 중 두번째 성질을 이용하면, 연산 과정 이후 나머지 연산을 실행해야하는 경우, 연산 중간에 나머지 연산을 함으로써 오버플로우가 발생하는 것을 막을 수 있다.

분할정복을 이용한 거듭제곱
어떤 정수 A의 B제곱을 구하고 싶다면 A를 B번 곱하면된다. 하지만 B가 매우 커지는 경우, 시간복잡도가 O(N)인 이 방식은 부담이 될 수도 있다. 하지만 분할정복 알고리즘을 이용하면 O(logN)에 거듭제곱 값을 구할 수 있다.
거듭제곱은 다음과 같이 표현할 수 있으며, 해당 식과 분할정복 알고리즘을 이용하여 각 N/2제곱에 해당하는 제곱 값을 한 번씩만 반환하면 N제곱을 구할 수 있다.
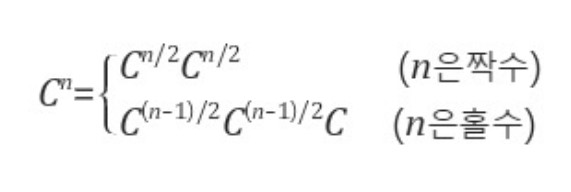
도가뉴의 항등식
N번째 피보나치 값을 구할 때 선형적인 방식을 이용해 값을 구하면 된다. 하지만 N이 매우 커지는 경우(10^18번째와 같이), 시간복잡도가 O(N)인 이 방식은 부담이 될 수도 있다. 하지만 도가뉴의 항등식을 이용하면 O(logN)에 N번째 피보나치 값을 구할 수 있다.
도가뉴의 항등식은 다음과 같다.

위의 항등식을 이용해서 정리하면 다음과 같이 정리된다.
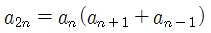
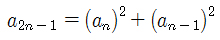
두 항등식을 이용해 N이 짝수일 때, 홀수일 때 적용하여 분할정복 알고리즘에 적용하면 N번째 피보나치 수를 구할 수 있다.
참고 자료:
- https://velog.io/@qkre/%EB%B0%B1%EC%A4%80-%ED%8C%8C%EC%9D%B4%EC%8D%AC-%EA%B3%A8%EB%93%9C-2-11444.-%ED%94%BC%EB%B3%B4%EB%82%98%EC%B9%98-%EC%88%98-6
- https://blog.naver.com/lovingasal/221676326121
오늘의 Trouble Shooting
- 오늘은 해결한 Trouble이 없어요!
오늘 하루는?
- 주말이고하니 뜸하게 풀었던 알고리즘 문제를 다시 풀기 시작했다. 오래전부터 한 번 쯤은 풀어봐야지' 했던 유형 중 하나인 분할정복을 이용한 거듭제곱 문제를 2개 풀었다. 해당 유형의 문제들은 수학적인 내용과 관련해서 나오는 경우가 많았기 때문에 조금 애를 먹었지만 증명만 하지 않고 활용만 하는 레벨이라면 적용하는 데 큰 문제는 없었다. 역시 알고리즘은 이렇게 한 유형씩 알아가는 재미가 쏠쏠하다.
오늘 푼 백준 문제
https://www.acmicpc.net/problem/1629
https://www.acmicpc.net/problem/11444
'Today I Learn' 카테고리의 다른 글
| [TIL] 240514 캠프 30일차: 개운한 결과물, 어지러운 머리 (0) | 2024.05.14 |
|---|---|
| [TIL] 240513 캠프 29일차: Node.js 시작 (0) | 2024.05.13 |
| [TIL] 240510 캠프 26일차 : 증식하는 공부거리 (0) | 2024.05.10 |
| [TIL] 240509 캠프 25일차 : 팀 프로젝트 끝! (0) | 2024.05.09 |
| [TIL] 240508 캠프 24일차 : defer, async, module, import/export (0) | 2024.05.08 |




